Stress-Based Fatigue Models

where k and f are material parameters, Δτ is the maximum shear stress range on a plane, and σn is the largest normal stress on the same plane. The plane that maximizes the left-hand side of the equation is considered to be critical.

The fatigue usage factor, fus, is the ratio between the left-hand side of the Findley criterion and the material parameter f. A value below 1 means that the component is loaded below the fatigue limit. For high compressive stress states the contribution from the normal stress can dominate the criteria predicting a negative fus. In those cases, the fatigue usage factor is set to zero.

To find the two material parameters k and f, two fatigue tests with different loading conditions are needed. This can, for example, be pure tension and pure torsion, but there are also other possibilities. For axial loading, the following relation is valid:

Here, σmax and σmin are the maximum and minimum stresses at the fatigue limit, respectively (that is, infinite life). Tests with two different R values can thus be used to determine k and f. In a pure (fully reversed) torsion test with an amplitude τa of the torsional shear stress, the corresponding relation is

If only uniaxial test data with a single R value is available, it is possible to estimate k from the ratio between the fatigue limits under different conditions for a similar material.

The Matake criterion is very similar to the Findley criterion. The difference is that it is the plane with maximum shear stress range that is taken as the critical plane, and the maximum normal stress is evaluated on that plane. The expression is:

At high compressive stress states when the Matake relation becomes negative, just as for Findley criteria, the fatigue usage factor is set to zero.

In the maximum normal stress criterion, the contribution from the shear stress is ignored and the plane which experiences the maximum normal stress range, Δσn, is considered as the critical plane. The criterion is defined with following expression

This is a one parameter criterion where only the fatigue limit in tension is needed. In order to match a simple uniaxial test, the fatigue limit should include any mean stress effects.

	This criterion is not suitable for materials or loadings where the mean stress is important.

The Dang Van model combines the observations of the importance of the shear stress on the crack nucleation and the influence of the hydrostatic stress on the crack propagation via relation

where τmax is the maximum shear stress, σH is the hydrostatic stress, while aDV and bDV are material constants.

The stress state at the macroscopic level, Σij, differs from the stress state at the microscopic level, σij. At the macroscopic level the material is homogeneous, while at the microscopic level it is inhomogeneous. According to the Dang Van theory, the two stress tensors are related to each other via a plastic shakedown that prevents crack growth from a critical grain to the neighboring one. Affected by the multiaxial loading, the material undergoes combined kinematic and isotropic hardening and as a result the center and the radius of the yield surface changes. The center of the smallest hypersphere in stress space which encloses the entire load history determines the residual stress tensor of the shakedown. It is a 6 dimensional hypersphere with the axes

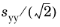
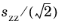
, sxy, syz, and sxz, where sij is the deviatoric stress tensor. The resulting microscopic stress is given by

where ρ is the residual stress tensor of the shakedown. A schematic description of the residual stress tensor for a biaxial case is shown in Figure 3-13.

The maximum shear stress is evaluated as

and the hydrostatic stress is evaluated as

where σ1, σ2, and σ3 are the principal stresses. The function argument t denotes the time dependence of the stress variables. The fatigue usage factor is finally computed as