Most of the structural applications operate in the elastic regime. Local inelastic deformation can however occur at stress concentrations. Although it is concentrated to a small volume, repeated increase in inelastic strains can introduce a crack. Once a crack is formed, it is easily driven by low stresses. The fatigue is said to be strain-controlled, since the stress will be limited above the yield stress, and will thus not be good indicator of the severity of the loading. A fatigue limit based on constant strain conditions is necessary for this type of analysis. The data can be obtained from strain-controlled tests rather than from stress-controlled tests. Figure 3-11 shows a fatigue result for such a test, where εa is the strain amplitude and N is the number of cycles to failure.

where Δε is the strain range evaluated as the difference between the largest and the smallest strain experienced during a fatigue cycle.

The fatigue limit in the strain-life relation is usually obtained using uniaxial tests, where strain amplitude is measured in one direction. In reality strain is a second order tensor. Therefore, the strain amplitude can be evaluated in different ways. In the E-N curve Model and the Combined Basquin and Coffin Manson Model the strain is evaluated according to

where ε1 is the largest principal strain, ε3 is the smallest principal strain.

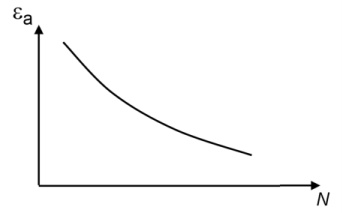
The E-N curve is a relation between strain amplitude, εa, and fatigue life, N, that can be summarized on the form

where fEN is the function. At low strain the fatigue life is limited by a Cycle Cutoff. At high strain when the strain amplitude exceeds the highest strain as defined by the E-N curve the fatigue life cannot be determined. No results are computed in such regions. This is demonstrated in Figure 3-12.

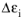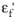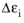
where is the accumulated inelastic strain in a load cycle, and c are material constants, and 2Nf is the number of load reversals to failure. Two reversals are equal to one cycle, so Nf is the number of cycles to failure. The fatigue relation in the original work (Ref. 5) was used for low-cycle fatigue prediction in metals and, therefore, was taken as the plastic strain range.

At low strains the fatigue life is limited by a Cycle Cutoff.

Many other fatigue models are based on the work by Coffin-Manson. These, however, express the damaging inelastic strain in various ways such as equivalent creep strain range, plastic shear strain, equivalent secondary creep, and others (Ref. 4). The original relation has been generalized in the Fatigue Module so that the accumulated inelastic strain can be evaluated in several ways depending on the selected Strain type in the Fatigue Model Selection section. 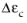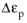The different options are shown in Table 3-4 where is the equivalent creep strain range and is the equivalent plastic strain range. When User defined is used as Strain type, the strain variable must be specified.

where σ'f is the fatigue strength coefficient, b is the fatigue strength exponent, ε'f is the fatigue ductility coefficient, c is the fatigue ductility exponent, and E is Young’s modulus. 2Nf is the number of load reversals, and thus Nf is the number of full cycles to failure at a strain amplitude of εa. At low strains the fatigue life is limited by a Cycle Cutoff.

where σm is the mean stress of the load cycle. Since stress is a second order tensor and the mean stress is a scalar, the evaluation of the mean stress is based on the principal stress according to