The L-VEL (Length-VELocity) turbulence model is an algebraic turbulence model often used in electronic cooling applications. It is less mesh sensitive than transport-equation models like Spalart-Allmaras or the k-ε model. It was developed by Agonafer et al. (Ref. 23) for internal flows and uses an extension of the logarithmic law of the wall which applies all the way down to the wall

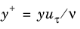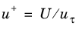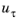
where , , U is the local flow speed, y is the distance to the nearest wall, ν is the kinematic viscosity and is the friction velocity. κ is the von Kàrman constant and E=8.6 is another constant needed to fit the logarithmic law of the wall. The shear stress in the wall layer is given by

Differentiating Equation 3-73 with respect to y+, the dimensionless effective viscosity is obtained as

If the local value of u+ is known, the effective viscosity can be evaluated from Equation 3-74. The value of u+ is obtained by forming a local Reynolds number

where the last expression follows from Equation 3-73. Hence, the nonlinear algebraic Equation 3-75 has to be solved at each node point to evaluate the effective viscosity. The local Reynolds number Re = Uy/ν is formed with the local absolute value of the velocity and the distance to the nearest wall. This implicitly assumes that the main flow direction is parallel to the wall.

The wall distance, y is provided by a mathematical Wall Distance interface that is included when using the L-VEL model. The solution to the wall distance equation is controlled using the parameter lref. The distance to objects larger than lref is represented accurately, while objects smaller than lref are effectively diminished by appearing to be farther away than they actually are. This is a desirable feature in turbulence modeling since small objects would get too large an impact on the solution if the wall distance were measured exactly.

The most convenient way to handle the wall distance variable is to solve for it in a separate study step. A Wall Distance Initialization study type is provided for this purpose and should be added before the actual Stationary or Time Dependent study step.

The L-VEL turbulence model is consistent with a no slip boundary condition; that is, u = 0. Since the turbulence model is algebraic, no additional boundary condition is needed. This boundary conditions is applied for Wall Treatment equal to Low Re.

The L-VEL model can be considered to be well resolved at a wall if is of order unity. is the distance, measured in viscous units, from the wall to the center of the wall adjacent cell and can be evaluated as the boundary variable: lplus_cc.

The default boundary treatment for Algebraic yPlus is the Automatic wall treatment. The details are described in Wall Boundary Condition for The Algebraic yPlus Turbulence Model.

See also Wall for boundary condition details.