The algebraic yPlus turbulence model is an algebraic turbulence model based on the distance to the nearest wall. The model is based on Prandtl’s mixing-length theory and is suitable for internal flows. It is less mesh sensitive than transport-equation models like Spalart-Allmaras or the k-ε model. In what follows, let y be the coordinate normal to the wall, and U the velocity parallel to the wall. Using a mixing length formulation, the balance for the shear stress in the wall layer may be approximated as

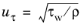
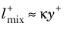
where y+ = yuτ/ν, u+ = U/uτ and is the friction velocity. Close to the wall, the mixing length must be zero such that u+ = y+, and far away from the wall, such that u+ = (1/κ)log(y+) + B. To obtain the correct behavior, the mixing length is chosen to be

where y* is to be determined. Inserting Equation 3-68 into Equation 3-67

For large values of y+, Equation 3-70 reduces to

the value of the constant y* is obtained as

This requires the local value of y+, which is obtained from the Reynolds number

The nonlinear algebraic Equation 3-72 has to be solved at each node point to evaluate the effective viscosity from Equation 3-71. The local Reynolds number Re = Uy/ν is formed with the local absolute value of the velocity and the distance to the nearest wall. This implicitly assumes that the main flow direction is parallel to the wall.

The wall distance, y is provided by a mathematical Wall Distance interface that is included when using the Algebraic yPlus model. The solution to the wall distance equation is controlled using the parameter lref. The distance to objects larger than lref is represented accurately, while objects smaller than lref are effectively diminished by appearing to be farther away than they actually are. This is a desirable feature in turbulence modeling since small objects would get too large an impact on the solution if the wall distance were measured exactly.

The most convenient way to handle the wall distance variable is to solve for it in a separate study step. A Wall Distance Initialization study type is provided for this purpose and should be added before the actual Stationary or Time Dependent study step.

The Algebraic yPlus turbulence model is consistent with a no slip boundary condition, that is u = 0. Since the turbulence model is algebraic, no additional boundary condition is needed. This boundary conditions is applied for Wall Treatment equal to Low Re.

The low-Reynolds-number formulation of the Algebraic yPlus model can be considered to be well resolved at a wall if is of order unity. is the distance, measured in viscous units, from the wall to the center of the wall adjacent cell and can be evaluated as the boundary variable: lplus_cc.

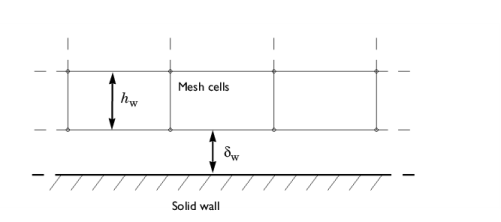
The default boundary treatment for Algebraic yPlus is the Automatic wall treatment. The automatic wall treatment assumes that there is a small gap, δw = hw/2, between the computational domain and the physical wall. Here, hw is the height of the mesh cell adjacent to the wall. wall (see Figure 3-7).

The boundary conditions for the velocity is a no-penetration condition u ⋅ n = 0 and a shear stress condition

The automatic wall treatment tends to the low-Reynolds-number formulation when hw tends to zero, and it becomes a wall function formulation when the resolution in viscous units, Δw+ increases. The resolution in viscous units is available as a postprocessing variable, Delta_wPlus.

See also Wall for boundary condition details.