Poroacoustics

The node defines a fluid domain with a porous material modeled in a homogenized way using a so-called equivalent fluid model. Several models exist to define the attenuation and dispersion experienced by the pressure waves as they propagate in the porous domain. The different models are described below.


	About the Poroacoustics Models

Poroacoustics Model

Select a : (the default), , , , , , , , , or .

Fluid Properties

Enter the properties of the saturating fluid that is inside of the porous material. These settings are common to most porous models. By default the uses the .

The following properties are available based on the selected above. The default values are taken . For enter a different value or expression.

•

c (SI unit: m/s) of the saturating fluid.

•

ρf (SI unit: kg/m3) of the saturating fluid (the fluid density).

If any other than the default is selected, the following properties are also required, depending on the selection. These material parameters are necessary as the more advanced models include the losses associated with viscosity and thermal conduction in a more or less detailed way:

•

Cp (SI unit: J/(kg·K)).

•

γ (dimensionless).

•

k (SI unit: W/(m·K)).

•

μ (SI unit: Pa·s).

•

Kf (SI unit: Pa).


	The implemented poroacoustics models are all applicable for any fluid, except the empirically determined Delany-Bazley-Miki model, which applies only to air. See Ideal Gas and General Fluid Options for details.

Porous Matrix Properties

In this section, enter the properties that describe the porous material. By default the uses the (the material defined for the domain). Select another material as needed. For example, create your own material that contains the properties of a given porous material and refer to it here. Here you also select if you want to use a rigid frame approximation or a limp frame approximation for the porous material (where applicable). The poroacoustic model defines complex-valued frequency-dependent expressions for both the bulk modulus and the equivalent density.

Based on the selected, enter the following settings for the porous matrix.

•

•

•

•

•

Johnson-Champoux-Allard

•

Johnson-Champoux-Allard-Lafarge

•

Johnson-Champoux-Allard-Pride-Lafarge

•

Three-Parameter Approximation JCAL Model

•

Williams Effective Density Fluid Model (EDFM)

•

Wood

Delany-Bazley-Miki

The Delany-Bazley-Miki model is an empirical model used to describe fibrous materials such as rockwool or glass fiber. The model can be used for materials with a porosity, εp, close to one. For , the Rf (SI unit: Pa·s/m2) uses values . For , enter a value or expression.

Select an option from the list: (the default), , , , , , , , , or . For enter values in the to fields. The models are empirical and based on fitting to measured data. This means the models have different regions of applicability with respect to the flow resistivity Rf, the frequency f, the material type, and the parameter X defined as

All the models are applicable for materials with a porosity εp close to 1. The model informations are listed in Table 2-2. See also Ref. 23 and the relevant section in About the Poroacoustics Models for further details.

Table 2-2: Delany-Bazley-Miki model options and applicability
Model name	Applicability
Delany-Bazley	Glass and rock wool with:
Miki	Glass and rock wool with:
Qunli	Porous plastic and open foams:
Mechel, glass fiber, low X	Glass fiber:
Mechel, glass fiber, high X	Glass fiber:
Mechel, rock fiber, low X	Rock fiber:
Mechel, rock fiber, high X	Rock fiber:
Komatsu	Glass and rock wool:
Modified Allard and Champoux


	Flow resistivity Rf is easy to measure and is independent of frequency.


	Absorptive Muffler: Application Library path Acoustics_Module/Automotive/absorptive_muffler

Zwikker-Kosten

The Zwikker-Kosten model is a two-parameter semiempirical model. It is one of the earliest equivalent fluid models for porous materials. The model assumes that the pores are cylinder-like with an effective hydraulic radius Hr. See Ref. 15 and About the Poroacoustics Models for further details.

For , select a : (the default) or . Then based on your choice, the default value for each of the following parameters is taken . For , enter another value or expression.

•

εp (dimensionless).

•

Hr (SI unit: m).

•

ρd (SI unit: kg/m3).

Attenborough

The Attenborough model is also based on the cylindrical-like pore assumption. It is a so-called four-parameter semiempirical model. The model is an extension of the Zwikker-Kosten model and has two additional input parameters. It accounts for the tortuosity (high frequency limit) τ∞, which is related to the orientation of the pores relative to the propagation direction. The hydraulic diameter of the pores is replaced by an expression that included the flow resistivity Rf and a fitting parameter b (this parameter is related to the anisotropy of the pore distribution). See Ref. 9, Ref. 16, and About the Poroacoustics Models for details.

For , select a : (the default) or . Then based on your choice, the default value for most of the following parameters is taken . For , enter another value or expression.

•

εp (dimensionless).

•

Rf (SI unit: Pa·s/m2).

•

(high frequency limit) τ∞ (dimensionless). The default is 1.

•

b (dimensionless). The default is 1.

•

ρd (SI unit: kg/m3).

Wilson

The Wilson model is a generalization of the semianalytical models for porous materials with constant cross section and parallel pores. This model is intended to match the middle frequency behavior of a porous material. See Ref. 17, Ref. 9, Ref. 18, and About the Poroacoustics Models for further details.

For , select a : (the default) or . Then based on your choice, the default value for the following parameters is taken . For , enter another value or expression.

•

εp (dimensionless).

•

(SI unit: Pa).

•

(SI unit: kg/m3).

•

τent (SI unit: s).

•

τvor (SI unit: s).


	Approximate expressions for the two relaxation times that are based on intrinsic material properties are given in the theory section for the Wilson model.

Johnson-Champoux-Allard

The Johnson-Champoux-Allard (or JCA model) is a five-parameter semiempirical model for describing a large range of porous materials with rigid (or limp) frames. As input, the model requires the viscous Lv and thermal Lth characteristic lengths (sometimes denoted Λ and Λ'). These replace the hydraulic radius used in simpler models and account for the thermal and viscous losses that appear at the acoustic boundary layer at pore walls. See About the Poroacoustics Models for details.

For , select a : (the default) or . Then based on your choice, the default value for most of the following parameters is taken . For , enter another value or expression.

•

εp (dimensionless).

•

Rf (SI unit: Pa·s/m2).

•

From the list:

Select (the default)to directly enter an expression for Lv (SI unit: m). The default expression is sqrt(acpr.mu*acpr.tau*8/(acpr.Rf*acpr.epsilon_p)), which corresponds to s = 1.

Select to enter a value for s (dimensionless) (the default is 1).

•

Lth (SI unit: m). The default expression is 2*acpr.Lv.

•

(high frequency limit) τ∞(dimensionless). The default is 1.

•

ρd (SI unit: kg/m3).


	The Johnson-Champoux-Allard (JCA) model with a rigid (motionless) frame (skeleton) is sometimes referred to as a Biot equivalent fluid model with a rigid porous matrix.

Johnson-Champoux-Allard-Lafarge

The Johnson-Champoux-Allard-Lafarge (or JCAL model) is an extension to the JCA model. It introduces corrections to the bulk modulus thermal behavior at low frequencies which is not captured by the JCA model. It introduces the static thermal permeability 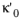parameter

and, thus, has one more parameter than the JCA model. It is a six-parameter semiempirical model. See Ref. 13, Ref. 9, and About the Poroacoustics Models for further details.

For , the settings are the same as for Johnson-Champoux-Allard with the addition of the

(SI unit: m2) setting.

Johnson-Champoux-Allard-Pride-Lafarge

The Johnson-Champoux-Allard-Pride-Lafarge (or JCAPL model) further extends the JCAL models by introducing a static viscous τ0 and thermal τ'0 tortuosity.

For , the settings are the same as for Johnson-Champoux-Allard plus these additional parameters:

•

τ0 (dimensionless). The default is 1.

•

τ'0 (dimensionless). The default is 1.

•

(SI unit: m2).

Three-Parameter Approximation JCAL Model

The represents an approximation to the JCAL model. Instead of requiring 6 parameters as input for the porous matrix it only requires three. The porosity as well as two parameters that relate to the topology of the pores are needed (their size and distribution). Two different approximation methods exist for the density and bulk modulus. Select the to either (the default) or . Then if necessary enter the values for (default is ):

•

εp (dimensionless).

•

(SI unit: m).

•

σs (dimensionless).

Details about the model can be found in Ref. 56, 57, 58, 59, and 60.

Williams Effective Density Fluid Model (EDFM)

is an effective density fluid model (EDFM) used to model the propagation of acoustic waves in sediments. The model assumes that the bulk and shear moduli of the frame of the porous material are negligible, meaning that the porous frame is limp. See Ref. 24 and About the Poroacoustics Models for further details.

The (the properties for the sediment) for have the default values taken . For , enter another value or expression:

•

ρgr (SI unit: kg/m3).

•

Kgr (SI unit: Pa).

•

εp (dimensionless).

•

(high frequency limit) τ∞ (dimensionless). The default is 1.

•

κp (SI unit: m2).

•

Hr (SI unit: m).

Wood

The model is used for a fluid mixture or a fluid suspension (solid inclusions completely surrounded by fluid). The Woods formula for the sound velocity is determined by using the effective bulk modulus of the suspension and the volume average density. As the Williams EDFM, this model gives effective values for the mixture. This model is exact for low frequencies, when the wavelength is much larger than the size of the inclusions. See Ref. 25 and About the Poroacoustics Models for further details.

The (the properties for the inclusions) for the model are entered in the table. For each (any number of inclusions can be added, the number is automatically incremented) enter the , the , and the . Add a new row (inclusion) by clicking the plus sign below the table. The table may be saved or loaded from a file.