You are viewing the documentation for an older COMSOL version. The latest version is
available here.
Tsai and Wu (Ref. 7,
Ref. 16) proposed a stress-dependent criterion intended at modeling failure in composites. Under Tsai-Wu criterion, failure occurs when a given quadratic function of stress is grater than zero. The failure criterion is given by
here, σ is the stress tensor,
F a fourth rank tensor (SI unit: 1/Pa^2) and
f is a second rank tensor (SI unit: 1/Pa). For Tsai-Wu criterion, failure occurs when
g(σ) ≥ 0.
Certain constraints ensure that the failure surface g(σ) =
0 forms a closed ellipsoid in the stress space. Also, thermodynamic considerations restrict the value of some components of the fourth rank tensor to be positive only. These restrictions are summarized as (no summation of the indexes)
The failure index is computed from the failure criterion as
The damage index is given by a boolean expression based on the failure criterion
here di =
1 means damage, and
di =
0 represents a healthy material.
The safety factor, also called
reserve factor or strength ratio, is computed by scaling the stress tensor such as the failure criterion is equal to zero
For an isotropic criterion, such as von Mises criterion, g(σ) =
σmises/σts − 1, and the safety factor is given by
sf =
σts/σmises.
The margin of safety (
Ref. 16) is then computed from the safety factor
Use the Safety subnode to set up variables which can be used to check the risk of failure according to various criteria. It can be used in combination with
Linear Elastic Material,
Layered Linear Elastic Material, or
Nonlinear Elastic Materials.
For this criterion, enter twenty one coefficients to define the 6-by-6 matrix F, and six coefficients to define the vector
f. The failure criterion is evaluated from the expression
here, σij are the stress tensor components given in the local coordinate system of the parent node.
For this criterion, enter nine coefficients corresponding to the tensile strengths σtsi, compressive strengths
σcsi, and shear strengths
σssij given in the local coordinate system of the parent node. Tsai-Wu coefficients are then computed from
all the other coefficients in F and
f tensors are set to zero.
For this criterion, enter six coefficients corresponding to the tensile strengths σtsi and shear strengths
σssij given in the local coordinate system of the parent node. Tsai-Wu coefficients are then computed from
For this criterion, enter nine coefficients corresponding to the tensile strengths σtsi, compressive strengths
σcsi, and shear strengths
σssij given in the local coordinate system of the parent node. Tsai-Wu coefficients are then computed from
all the other coefficients in F and
f tensors are set to zero.
Enter nine coefficients corresponding to the tensile strengths σtsi, compressive strengths
σcsi, and shear strengths
σssij given in the local coordinate system of the parent node. The failure criterion is then computed from
here, εsi is either the tensile strength or the compressive strength depending whether the stress in the
i direction,
σi, is positive or negative. The absolute value of the shear stress
σij in the
ij-plane is compared to the corresponding shear strength
σssij.
here, εsi is either the ultimate tensile strain or the ultimate compressive strain depending whether the strain in the
i direction,
εi, is positive or negative. The absolute value of the shear strain
γij in the
ij-plane is compared to the corresponding ultimate shear strain
γssij.
This criterion is derived from Tsai-Wu theory for two-dimensional plane stress problems (Ref. 17). It is available in 2D for the Pate interface and the Solid Mechanics interface in plane stress, and for the Shell interface in 3D. Enter the coefficients corresponding to the tensile strengths
σtsi, compressive strengths
σcsi, and shear strengths
σssij given in the local coordinate system of the parent node. The failure criterion is then computed from the in plane stresses
all the other coefficients in F and
f tensors are set to zero.
all the other coefficients in F and
f tensors are set to zero.
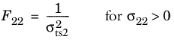 , or
, or 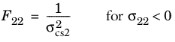
all the other coefficients in F and
f tensors are set to zero.
The effective von Mises stress σmises is defined from the deviatoric stress tensor, see the section about plasticity and
von Mises Criterion. For ductile materials the tensile strength corresponds to the yield stress, while for brittle materials it corresponds to the failure strength.
here, Tresca equivalent stress is defined in terms of principal stresses, σtresca =
σ1 − σ3, see
Tresca Criterion. For ductile materials the tensile strength corresponds to the yield stress, while for brittle materials it corresponds to the failure strength.
here, σs is either the tensile strength or the compressive strength depending whether the principal stress,
σpi, is positive or negative. For ductile materials the tensile strength corresponds to the yield stress, while for brittle materials it corresponds to the failure strength.
here, εs is either the ultimate tensile strain or the ultimate compressive strain depending whether the principal strain,
εpi, is positive or negative. For ductile materials the ultimate tensile strain corresponds to the strain at yielding, while for brittle materials it corresponds to the strain at failure.
The material parameters α and
k are related to the cohesion
c and angle of internal friction
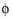
in the Mohr-Coulomb criterion, see
Drucker-Prager Criterion for details. Also, the cohesion and the angle of internal friction can be related to the tensile and compressive strengths, see
Mohr-Coulomb Criterion for details. The failure index is computed from
The parameters k1,
k2, and
k3 are computed from the uniaxial compressive strength
σc, the uniaxial tensile strength
σt, and the biaxial compression strength
σb, see
Bresler-Pister Criterion for details. The failure index is computed from
here, σc is the uniaxial compressive strength,
σt is uniaxial tensile strength, and
σb is the biaxial compressive strength. The function
r(
θ) describes the segment of an ellipse on the octahedral plane, see
Willam-Warnke Criterion for details. The failure index is computed from
In this formulation, the parameters a and
b are positive and dimensionless, and
σc is the uniaxial compressive strength for concrete (also with a positive sign). The dimensionless function
λ(
θ) depends on the Lode angle
θ and two positive parameters
k1 and
k2, see
Ottosen Criterion for details. The failure index is computed from
You can add any number of Safety nodes to a single material model. The contents of this feature will not affect the analysis results as such, as this feature does not account for post-failure analysis. You can add
Safety nodes after having performed an analysis and just do an
Update Solution in order to access to the new variables for result evaluation.
Table 3-6 shows failure criterion and considered failure modes by that criterion. .
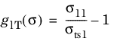 for
for 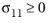
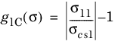 for
for 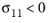
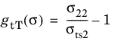 for
for 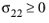
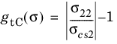 for
for 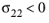
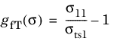 for
for 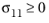
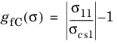 for
for 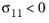
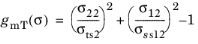 for
for 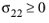
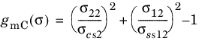 for
for 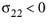
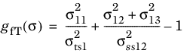 for
for 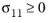
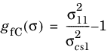 for
for 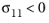
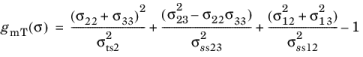 for
for 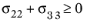
for 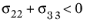
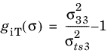 for
for 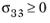
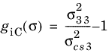 for
for 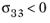
For plane stress conditions, the Hashin criterion is modified by setting σ13 =
σ23 =
σ33 = 0. With 2D plane stress version of Hashin criterion, the interlaminar failure cannot be predicted.
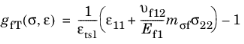 for
for 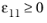
where Ef1 and
νf12 are Young’s modulus of fiber in longitudinal direction and in-plane Poisson’s ratio of fiber, respectively, and
mσf is the mean stress magnification factor.
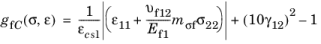 for
for 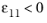
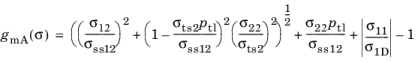 for
for 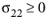
where ptl is slope of the in-plane fracture envelope in tension and
σ1D is linear degradation stress.
where pcl is slope of the in-plane fracture envelope in compression,
RAtt is fracture resistance against transverse shear loading and
σcss12 is modified shear strength.
where pct is slope of the transverse fracture envelope in compression.
This criterion is used for accurate predicting the failure of unidirectional FRP laminates with in-plane stress state. This is one of the most advanced failure criteria composed of six phenomenological failure modes describing matrix and fiber failure accurately without the use of curve-fitting parameters (Ref. 20). This criterion assumes a fragile fracture for the matrix failure in compression and implements the action plane concept according to the Mohr–Coulomb theory. This failure theory considers failure modes based on the fiber kinking due to misalignment and on the tensile matrix cracking associated with interlaminar crack propagation.
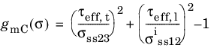 for
for 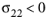
where τeff,t and
τeff,l are effective shear stresses in transverse and longitudinal directions, respectively, and
σiss12 is longitudinal in situ shear strength. The effective shear stresses are functions of the fracture plane angle which is found out by maximizing the Mohr-Coulomb effective stresses.
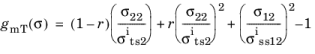 for
for 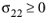
where σits2 is in situ tensile strength, and r is a material constant based on fracture toughness.
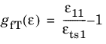 for
for 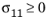
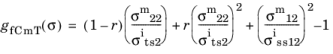 for
for 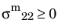
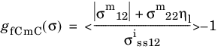 for
for 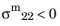
where σmij are the ply stresses transformed in the misalignment coordinate frame, and
ηl is a non-dimensional parameter based on the failure strength and fracture plane angle under uniaxial transverse compression.
where the effective shear stresses in transverse and longitudinal directions, τmeff,t and
τmeff,l, are calculated from stresses in the misalignment coordinate frame.