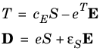Piezoelectric Material

The direct piezoelectric effect consists of an electric polarization in a fixed direction when the piezoelectric crystal is deformed. The polarization is proportional to the deformation and causes an electric potential difference over the crystal.

The inverse piezoelectric effect, on the other hand, constitutes the opposite of the direct effect. This means that an applied potential difference induces a deformation of the crystal.

It is possible to express the relation between the stress, strain, electric field, and electric displacement field in either a stress-charge form or strain-charge form:

In the above relations, the naming convention used in piezoelectricity theory is assumed, so that the structural strain is denoted by S, and the stress is denoted by T. Thus, the naming convention differs in piezoelectricity theory compared to structural mechanics theory.

	The Piezoelectric Material uses the structural mechanics nomenclature. The strain is named ε (instead of S) and the stresses are denoted by either σ or S (instead of T). This makes the names consistent with those used in the other structural mechanics interfaces.

The constitutive relation using COMSOL Multiphysics symbols for the different constitutive forms are thus:

The Stress-Charge form is always used in the variational formulation (weak equation form) which COMSOL Multiphysics uses for discretization and computation.

Most material data appears in the strain-charge form, and it can be easily transformed into the stress-charge form. In COMSOL Multiphysics both constitutive forms can be used; simply select one, and the software makes any necessary transformations. The following equations transform strain-charge material data to stress-charge data:

You find all the necessary material data inputs within the Piezoelectric Material feature under the Solid Mechanics interface, which are added automatically when you add a predefined Piezoelectricity multiphysics interface. Such node can be also added manually under any Solid Mechanics interface similar to all other material model features. The piezoelectric material uses the Voigt notation for the anisotropic material data, as customary in this field. More details about the data ordering can be found in Orthotropic and Anisotropic Materials section.

The equations of Piezoelectricity combine the momentum equation Equation 3-94 with the charge conservation equation of Electrostatics,

where the ρV is the electric charge concentration. The electric field is computed from the electric potential V as

In both Equation 3-65 and Equation 3-94, the constitutive relations Equation 3-62 are used, which makes the resulting system of equations closed. The dependent variables are the structural displacement vector u and the electric potential V.

In case of geometric linearity, the governing equations for a linear piezoelectric medium of any anisotropy can be written in terms of the structural displacement vector u and electric potential V as:

The following symmetries hold for the constitutive tensor coefficients:

	Piezoelectric material data inputs in COMSOL Multiphysics are based on the matrix representation of higher-order tensors using Voigt notations. Thus, to obtain coefficients of 6-by-3 coupling matrix , the first index of the coupling tensor components remains the same, while the last two indexes should be replaced by a single index obtained using special rules. Similarly, for the stiffness tensor, the first pair and the second pair of indexes must be replaced by a single index used instead of each pair. See Orthotropic and Anisotropic Materials for the index transformation rules.

The constitutive relations in tensor notations can be derived using a thermodynamic potential called the electrical enthalpy:

Since the relations in Equation 3-66 are linear, they posses the following time-harmonic wave solutions:

where k = kn is the wave number vector, n is the direction vector that defines the wavefront propagation direction. The wavefront is an imaginary line connecting solid particles of the same phase. The velocity of such wavefront in the direction normal to it is given by the phase velocity c = ω/k.

A generalization of Christoffel’s equation (Equation 3-18) can then be done:

where the generalized Christoffel’s tensor is defined as

The generalized Christoffel’s equation can be considered as an eigenvalue problem. Thus, to have a nontrivial solution, the phase velocity must satisfy:

which is called the dispersion relation. This is in general case a cubic polynomial with three roots

. Thus, for an arbitrary anisotropic medium, three waves with different phase velocities can propagate in each given direction.

However, most piezoelectric materials exhibit only moderate degree of anisotropy. The material data is usually given in a coordinate system, in which it is ether orthotropic or even transverse isotropic where only one direction (poling direction) differs from the two others. In this case, the expressions for the phase velocity can be computed analytically for waves of certain types, polarizations and directions of propagations.

For example, the pressure wave propagating in the X-axis direction is a particular solution, for which

The corresponding phase velocity is given by

Here, the material data coefficients are given in the same matrix form notation that is used in COMSOL Multiphysics for data input.

The shear wave propagation in the X-axis direction and with XY-plane polarization is a solution such that

and the corresponding phase velocity is computed as

If the wave propagation is initiated by a small perturbation that is initially localized in space, the solution can be found using Fourier and Laplace transforms, and it will represent a so-called wave packet. The wave packet will propagate with the group velocity given by:

where un,j is the wave polarization vector that is the eigenvector corresponding to the eigenvalue solution

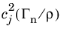
of the Christoffel’s equation.

COMSOL Multiphysics provides predefined variables for the phase and group velocities for waves of different types propagating in any chosen direction. These variables do not affect the solution as such, but are available during result presentation if the Wave Speeds node has been added to the material.

	The wave speed variables can be found in the Wave speeds folder under Solid Mechanics in the Replace Expression tree.

In order to define dissipation in the piezoelectric material for a time-harmonic analysis, all material properties in the constitutive relations can be complex-valued matrices where the imaginary part defines the dissipative function of the material.

Complex-valued data can be defined directly in the fields for the material properties, or a real-valued material X and a set of loss factors ηX can be defined, which together form the complex-valued material data

The sign in the complex damping terms are defined as

In the four first expressions, the choice of sign is a result of the single physics observations that

For these cases, it is thus necessary that ηX is positive in order for the material to be thermodynamically stable with the chosen signs.

The sign of the coupling losses requires more considerations, and the chosen sign must be considered as a definition. All values of ηe and ηd does not necessarily have to be positive. For some simple theoretical cases with isotropic loss factors, it can however be shown that the definition above is reasonable:

•

Consider a material which in strain-charge form only has mechanical damping. Thus, d is real, and the second transformation law in Equation 3-64shows that e must have a positive loss factor.

•

Consider a material with only coupling loss. Then the second transformation law in Equation 3-64 shows that d and e must have the same loss factor multiplier. From the third transformation law it can be inferred that ηe and ηd in this case must be positive in order for the material to have an appropriate phase lag between D and E.

In a real material, all types of losses occur simultaneously. Then, the criteria for allowable values of the loss factors become complicated, particularly if they are not isotropic.

It is also possible to define the electrical conductivity of the piezoelectric material, σ. Electrical conductivity appears as an additional term in the variational formulation (weak equation form). The conductivity does not change during transformation between the formulations.

The energy dissipation modeling is also available in time domain. The options are: dielectric dispersion for the electrical part, and Rayleigh damping for the mechanical and coupling parts of the problem. The total dissipated energy can be computed as a function of time.

	Piezoelectric Losses

Using the functionality available under the Piezoelectric Material feature and Solid Mechanics interface, one can define initial stress (S0), initial strain (ε0), and remanent electric displacement (Dr) for models. In the constitutive relation for piezoelectric material these additions appear in the stress-charge formulation: