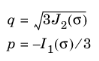You are viewing the documentation for an older COMSOL version. The latest version is
available here.
The Cam-Clay material model was developed in the 1970s at the University of Cambridge, and since then it has experienced different modifications. The modified Cam-Clay model (MCC) is the most commonly used model due to its smooth yield surface, and it is the one implemented in the Geomechanics Module.
This is an ellipse in the pq-plane, with a cross section independent of the Lode angle. Note that
p,
q, and
pc are positive variables.
The parameter M > 0 defines the slope of the
critical state line in the
pq-plane. This parameter can be related to the angle of internal friction
φ in the Mohr-Coulomb criterion as
(3-46)
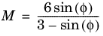
|
|
The slope of the critical state line M can either be a material property or it can be derived from the angle of internal friction φ.
|
|
|
The void ratio e is the ratio between the pore space and solid volume. It can be written in terms of the porosity ε as e = ε/(1−ε).
|
The compression index λ is the slope of the
virgin isotropic consolidation line, and the swelling index
κ is the slope of the
swelling line (also called unloading-reloading line) in the
e versus
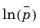
plane. The nondimensional pressure is written using the reference pressure
pref
where e0 is the initial void ratio calculated as
(3-47)
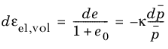
Integrating Equation 3-47, the equation is reformulated as
(3-48)
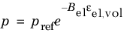
The secant bulk modulus Ks (or bulk modulus
K) is written as
(3-49)
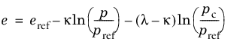
In the modified Cam-Clay model, hardening is controlled by the consolidation pressure pc, which depends on the volumetric plastic strain
εp,vol as
(3-50)
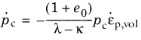
The evolution of the consolidation pressure depends on the values for the initial void ratio e0, the
swelling index κ, and the
compression index λ, which are positive parameters that fulfill
|
|
If an Initial Stress and Strain node is added to the Cam-Clay material, the initial consolidation pressure pc0 must be equal or larger than one third of minus the trace of the initial stress tensor, otherwise the initial stress state is outside the Cam-Clay ellipse.
|
Here, σ is the stress tensor,
ε is the total strain tensor,
εel is the elastic strain tensor,
σ0 is the initial or external stress tensor, and
C is the fourth-order elasticity tensor. Assuming an isotropic material, Hooke’s law simplifies to
Here, G is the shear modulus.
At zero volumetric strain and no loading, the pressure in the MCC model is equal to the reference pressure (see Equation 3-48). This is needed as the MCC model do not have stiffness at zero stress. The reference pressure appears as an additional term in the variational formulation (weak equation).
As opposed to the Linear Elastic Material, the MCC model introduces a nonlinear relation for the hydrostatic pressure as a function of the volumetric elastic strain given by
Equation 3-48.
The yield surface and the associated flow rule (Qp =
Fy) give the rate equation for the plastic strains. The plastic strain tensor
εp is calculated from the plastic multiplier
λp and the derivatives of the plastic potential
Qp with respect to the stress tensor
σ
This relation explains why there is isotropic hardening when the pressure is
p > pc/2 and
isotropic softening when
p < pc/2. As opposed to what happens in
J2 plasticity, in the modified Cam-Clay soil model the volumetric plastic strain can either increase or decrease as plastic deformation occurs.
When an external pore pressure pf is added to the MCC material, the yield function is shifted along the
p axis, and the yield function reads:
The quantity p − pf is normally regarded as the
effective pressure, or effective stress, which should not be confused with the von Mises stress. To add the effect of a fluid pressure in the pores
pf to the Modified Cam-Clay material, add an
External Stress feature.
The structured Cam-Clay model (SCC) was developed (Ref. 20,
Ref. 21) to circumvent the limitations of the Cam-Clay model when applied to structured soils and clays. The SCC model, however, does not consider the influence of the soil structure neither on strength characteristics (especially cohesion) nor in the softening behavior, and it is also not suitable to model cemented clays.
In the MSCC model, the reduction of mean effective stress due to structure degradation, pb, depends on the shear plastic strain
εp,dev. The destructuring mechanism is the process of reducing structure strength due to the degradation and crushing of the structure. The structure degradation is given by
(3-51)
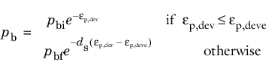
Here, pbi is the initial structural strength,
pbf the failure structural strength,
εp,devc is the effective plastic strain at failure, and
ds is the destructuring index due to shear deformation.
where is e void ratio of the structured clay,
Δe is additional void ratio,
e* is void ratio of the destructured clay at the same stress state. The void ratio can be found by using
Equation 3-49. Further,
Δei is the additional void ratio at consolidation pressure, and
dv is the destructuring index due to volumetric deformation.
Here, ς is a parameter to smooth the shape of the plastic potential. The slope of the critical state line,
M can be found by using
Equation 3-46.
Here λ* is the compression index for destructured clay,
κ is the swelling index, and
η is ratio of shear stress to mean stress.
At zero volumetric strain and no loading, the pressure of MSCC model is equal to reference pressure (see Equation 3-52). This is needed as the MSCC model does not have any stiffness at zero stress. The reference pressure appears as an additional term in the variational formulation (weak equation form).
Here, p and
q are stress invariants as defined in
The Modified Cam-Clay Soil Model,
pcs is the consolidation pressure at current suction,
ps is the tensile strength due to current suction,
s is the current suction,
b is a dimensionless smoothing parameter,
sy is the yield value at current suction, and
pref is the reference pressure at which the reference void ratio
eref was measured.
The tensile strength due to current suction, ps, is linearly related to the suction level as
ps =
ks, where
k is the tension to suction ratio.
where λ(s) is the compression index at current suction,
λ0 is the compression index at saturation, and
κ is the swelling index. The compression index at current suction,
λ(s), is given by
where w and
m are weighting and soil stiffness parameters.
As opposed to The Modified Cam-Clay Soil Model, the slope of the critical state line,
M, depends on both the Lode angle
θ and the angle of internal friction
φ.
As in The Modified Cam-Clay Soil Model, hardening is controlled by the evolution of the consolidation pressure
pc, which depends on the volumetric plastic strain
εp,vol.
(3-53)
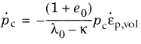
The initial void ratio e0, the swelling index
κ, and the compression index at saturation
λ0, are positive parameters.
The evolution of the yield value at current suction, sy, is also governed by the volumetric plastic strain
εpl,vol as
(3-54)
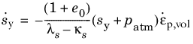
Here λs is the compression index for changes in suction,
κs is the swelling index for changes in suction, and
patm is the atmospheric pressure, all positive parameters. Note that
Equation 3-53 and
Equation 3-54 are normally given with opposite sign, but here we use the structural mechanics convention so the increments in consolidation pressure and suction are positive in compression.
Here K is the bulk modulus, and
Kcs the stiffness to suction. Note that the pressure
p in compression and suction
s is positive variables, but the elastic volumetric strain
εel,vol is negative in compression.The volumetric elastic response due to suction is given by
Here, s0 is the initial suction. The volumetric elastic response due to suction is accounted in the total strain tensor for BBMx model, so any changes in suction with keeping pressure constant can cause volumetric strains.
(3-55)
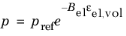
At zero volumetric strain at no loading, the pressure of BBMx model is equal to reference pressure (see Equation 3-52). This is needed as the BBMx model does not have stiffness at zero stress. The reference pressure appears as an additional term i the variational formulation (weak equation form).
|
|
Note that the variables λ0, λ(s), and λs are different. The material property λ0 is the compression index at saturation, which does not depends on the suction. The variable λ(s), which is a function of the current suction, is the compression index in the void ratio vs. natural logarithm of the mean stress plane. The material property λs is the compression index in the void ratio vs. natural logarithm of the matrix suction plane, which does not depends on the mean stress.
|
The stiffness moduli for primary loading, denoted by E50, and for unloading/reloading, denoted by
Eur, are given by
Here 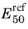 and
and  are reference stiffness moduli at reference pressure pref
are reference stiffness moduli at reference pressure pref,
c is the cohesion,
φ is the angle of internal friction, and
m is the stress exponent. The ultimate deviatoric stress
qf and the stress to failure
qa are derived from the Mohr-Coulomb criterion, and defined as
where Rf is the failure ratio. The yield function and plastic potential for the shear hardening cone are defined in terms of stress invariants, and given by
where γp is the accumulated plastic shear strain and
ψm is the mobilized dilatancy angle.
Here, Rc is the ellipse aspect ratio, and is given by
The internal variables pc and
γp depends on the volumetric plastic strain
εpl,vol and the plastic strain invariant
J2 (εpl), and their evolution is defined as
where H is the hardening modulus. The hardening modulus depends on the bulk modulus in compression
Kc and the bulk modulus in swelling
Ks, and is derived from
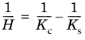 where
where 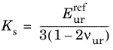
where C is a function of the stiffness modulus
Eur and Poisson’s ratio
ν.