The Thermionic Emission feature is used to release electrons from a hot cathode. It releases model particles from a boundary such that the emitted current density magnitude
Jth (SI unit: A/m
2) is (
Ref. 10)
The total current Ith (SI unit: A) released from the surface is
where vn is the velocity component normal to the cathode surface and
vt1 and
vt2 are the two orthogonal velocity components parallel to the surface. The azimuthal angle
ϕ is uniformly distributed in the interval
[0, 2π]. The polar angle
θ is
where U1 is a uniformly distributed random number in the interval
[0, 1]. The particle speed
V (SI unit: m/s) can be sampled from a probability distribution function in several different ways, which are described in the following section.
where me =
9.10938356 × 10-31 kg is the electron mass. The thermal electrons are assumed to be nonrelativistic. The probability distribution function of the normalized kinetic energy is
For Uniform Current the values of the normalized kinetic energy for the particles are sampled from
Equation 4-14 using the method of inverse transform sampling, in which the probability distribution function (PDF) is used to compute a cumulative distribution function (CDF) which is then normalized to unity and inverted (inverse normal CDF). When uniformly distributed random numbers in the interval
[0,1] are used as input to the inverse normal CDF, the resulting set of values follows the PDF.
where LambertW(−1, x) is the
−1 branch of the Lambert W function or product log, defined as the real root of the equation
U3 is a uniform random number in the interval
[0,1] that is uncorrelated with the random numbers used to initialize the polar angle
θ and azimuthal angle
φ.
Because the initial particle energy is sampled from the probability distribution function given in Equation 4-14, each particle carries the same weight; that is, each model particle is a macroparticle representing an equal number of electrons emitted per unit time. This macroparticle weighting is represented by a static degree of freedom stored for all model particles called the effective frequency of release
frel,
To yield the specified total current Ith, the effective frequency of release of the
ith model particle must be
where N (dimensionless) is the total number of model particles released by the feature.
When Uniform energy intervals is selected, the initial normalized kinetic energy of each particle is uniformly sampled from the interval
[0, n], where
n is a user-defined proportionality factor. Because the energy is uniformly sampled instead of following the probability distribution given by
Equation 4-14, the probability distribution must instead be incorporated into the effective frequency of release:
where the sum over j in the denominator is taken over all model particles released by the feature.
Equation 4-14 has a local maximum at
W = 1, after which it gradually decreases. Some representative values of the CDF are given in
Table 4-5.
Therefore a value of n = 10, for example, will encompass more than
99.9% of the cumulative distribution function.
When Uniform speed intervals is selected, the initial speed of each particle is uniformly sampled from the interval
[0, Vmax], where
where n (dimensionless) is a user-defined proportionality factor.
Therefore, compared to Equation 4-15 the proportionality factor is multiplied by an additional term proportional to
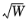
:
where again the sum over j in the denominator is taken over all model particle emitted by the feature.
The main motivation for selecting Uniform energy intervals or
Uniform speed intervals is that these options devote a disproportionately large number of degrees of freedom to electrons at the extreme ends of the probability distribution function. For example, when sampling from
Uniform energy intervals with
n > 8, equal representation would be given to particles in the neighborhood of
W = 1 and
W = 7.64, despite
W = 1 having a probability density
100 times more greater than
W = 7.64.