The Particle-Matter Interactions node is used to model interaction of energetic ions with solid material. The interaction of energetic ions with the target material is divided into two main interaction types: ionization losses and nuclear stopping.
The Ionization Loss node models the interaction of ions with the electrons in the target material as a continuous braking force:
Thus the force always acts opposite the direction of particle motion. For built-in ionization loss models empirical data from Ref. 1 is used to generate a 1D interpolation function, from which the stopping power is expressed as a function of the particle kinetic energy.
The Nuclear Stopping node models the interaction of ions with the nuclei in the target material. Unlike ionization losses, which are treated as a force that is continuous as a function of time, interactions with target nuclei are treated as distinct events that occur instantaneously with a given probability during each time step. In addition, nuclear interactions may change the direction of the ion velocity as well as its magnitude.
which is a dimensionless version of the expression for the scattering angle as given in Ref. 6, in which
b (dimensionless) is the reduced impact parameter and
ξ is the dimensionless energy defined as
where r (SI unit: m) is the radial distance from the particle trajectory to the target nucleus and
aI (SI unit: m) is the screening length. The definition of the screening length changes depending on the option selected from the
Screening function list; see
Table 4-3 below.
The reduced energy ε (dimensionless) is defined by the expression
The lower limit of integration ξmin (dimensionless) is the largest positive root of the equation
The screening function Φ(
χ) (dimensionless) changes depending on the option selected from the
Screening function list. The available options are tabulated below.
The value of the reduced impact parameter b is sampled from a Rayleigh probability distribution using the expression
where U is a dimensionless random number sampled with uniform probability from the interval
(0,1),
L is the distance traveled by the particle during the time step, and
N is the number density of particles in the target material. Thus it is clear that if very small time steps are taken by the solver, the value of
b is typically quite large. This in turn means that the scattering angle
χ is very close to
0, so most collisions tend not to have a large effect on the particle trajectory. If the computed value of
χ is less than the specified
Cutoff scattering angle χc, then the collision is deemed insignificant and the particle velocity is not reinitialized during that time step.
If the collision is considered significant, that is if 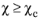 , then in addition to being deflected by the scattering angle, the reinitialized particle trajectory is also rotated by an azimuthal angle φ
, then in addition to being deflected by the scattering angle, the reinitialized particle trajectory is also rotated by an azimuthal angle φ that is sampled at random from the interval
[0, 2π]. A fraction of the particle energy is also lost to the surroundings; the kinetic energy
E of the particle decreases by the recoil energy
T, defined by the expression
where m1 and
m2 (SI unit: kg) are the ion mass and the atomic mass of the target material.
To avoid the computational cost of evaluating the integral in Equation 4-12 at every time step for every particle, the value of this integral is tabulated for a range of values of
b and
ε, then imported into models as a set of 2D interpolation functions. Thus, there is a finite range of values in which the nuclear stopping data is computed accurately, corresponding to the interval defined by the inequalities