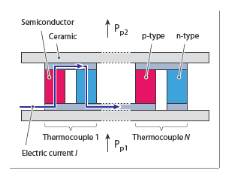

|
•
|
S (SI unit: V/K) is the Seebeck coefficient of the thermocouple
|
|
•
|
I (SI unit: A) is the electric current operating in the module
|
|
•
|
|
•
|
ΔT (SI unit: K) is the temperature difference between the two sides of the module
|
|
•
|
R (SI unit: K/W) is the thermal resistance of the thermocouple
|
|
•
|
|
•
|
P=-Q (removed heat)
|
|
•
|