Once you have a mesh, you can introduce approximations to the dependent variables. For this discussion, concentrate on the case of a single dependent variable, u. The idea is to approximate u with a function that you can describe with a finite number of parameters, the so-called degrees of freedom (DOF). Inserting this approximation into the weak form of the equation generates a system of equations for the degrees of freedom.

Start with a simple example: linear elements in 1D. Assume that a mesh consists of just two mesh intervals: 0 < x < 1 and 1 < x < 2. Linear elements means that on each mesh interval the continuous function u is linear (affine). Thus, the only thing you need to know in order to characterize u uniquely is its values at the node points x1 = 0, x2 = 1, and x3 = 2. Denote these as U1 = u(0), U2 = u(1), U3 = u(2). These are the degrees of freedom.

where are certain piecewise linear functions. Namely, is the function that is linear on each mesh interval, equals 1 at the ith node point, and equals 0 at the other node points. For example,

The 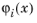are called the basis functions. The set of functions u(x) is a linear function space called the finite element space.

For better accuracy, consider another finite element space corresponding to quadratic elements. Functions u in this space are second-order polynomials on each mesh interval. To characterize such a function, introduce new node points at the midpoint of each mesh interval: x4 = 0.5 and x5 = 1.5. You must also introduce the corresponding degrees of freedom Ui = u(xi). Then, on each mesh interval, the second-degree polynomial u(x) is determined by the degrees of freedom at the endpoints and the midpoint. In fact, you get

where the basis functions now have a different meaning. Specifically, is the function that is quadratic on each mesh interval, equals 1 at the ith node point, and equals 0 at the other node points. For example,

In general, you specify a finite element space by giving a set of basis functions. The description of the basis functions is simplified by the introduction of local (barycentric) coordinates (or element coordinates) ξ i. Consider a mesh element of dimension d in an n-dimensional geometry (whose spatial coordinates are denoted x1,…, xn). Consider also the standard d-dimensional simplex

which resides in the local coordinate space parameterized by the local coordinates ξ1, …, ξd. If d = 1, then this simplex is the unit interval. If d = 2, it is a triangle with two 45 degree angles, and if d = 3 it is a tetrahedron. Now you can consider the mesh element as a linear transformation of the standard simplex. Namely, by letting the global spatial coordinates xi be suitable linear (affine) functions of the local coordinates, you get the mesh element as the image of the standard simplex.

When described in terms of local coordinates, the basis functions assume one of a few basic shapes. These are the shape functions. In the example with linear elements in 1D, any basis function on any mesh element is one of the following:

Thus the first two are the shape functions in this example (0 is not counted as a shape function). In the example with quadratic elements in 1D, the shape functions are

When using higher-order elements (that is, elements of an order > 1), the solution has a smaller error. The error also depends on how well the mesh approximates the true boundary. To keep errors in the finite element approximation and the boundary approximation at the same level, it is wise to use curved mesh elements. They are distorted mesh elements that can approximate a boundary better than ordinary straight elements (if the model’s boundary is curved). You can get curved mesh elements by writing the global coordinates xi as polynomials of order k (the geometry shape order) in the local coordinates ξj (the earlier example took k = 1). Then the mesh element is the image of the standard simplex. For mesh elements that are not near a boundary, there is no reason to make them curved, so they are straight. It is customary to use the same order k here as for the order of the (Lagrange) element. This is referred to as using isoparametric elements.

The order k   is determined by the geometry shape order for the frame (coordinate system) associated with the finite element. The frame is determined by the property frame to the finite element (the default is the reference frame). For certain finite elements, the geometry shape order given by the frame can be overridden by the property sorder. In the COMSOL Desktop, the default setting is to use an automatic geometry shape order, which means that the geometry shape order is equal to the highest order of any shape function used in the model.

The mesh element types available in COMSOL have the following representations in local coordinates ξ1, …, ξd: