A Bézier Polygon (
) consists of a sequence of connected line segments, quadratic Bézier curves (for example, circular arcs), and cubic Bézier curves. See
About Rational Bézier Curves below for some information about Bézier curves in general.
From the Type list, select
Solid,
Closed curve, or
Open curve to specify if the Bézier polygon is a solid object (only available in 2D) or a closed or open curve object. If you choose
Solid or
Closed curve, the software automatically adds a line segment if needed to close the polygon.
Define the Bézier polygon by adding curve segments to the list of segments. Choose linear segments, quadratic segments, or cubic segments. Delete segments by selecting them and clicking Delete. To edit a segment, select it in the list. When editing the last segment, click
Close Curve to make the last control point coincide with the first control point of the first segment.
To add a linear segment, click Add Linear. Specify the start of the linear segment on the first row of coordinates under
Control points. Specify the end of the linear segment on the second row of coordinates.
To add a quadratic segment, click Add Quadratic. Specify the coordinates of the three control points on rows under
Control points. Add the weights of the control points under
Weights. The default weights —
1,
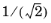
, and
1 — correspond to a circular arc if the control points are three corners of a square.
To add a cubic segment, click Add Cubic. Specify the coordinates of the four control points on each row under
Control points. Add the weights of the four control points under
Weights. Cubic segments with self-intersections might look correct when displayed but are not handled correctly by other geometry and meshing operations.
The coordinate system in which the segment coordinates above are interpreted. From the Work plane list, select
xy-plane (the default, for a standard global Cartesian coordinate system) or select any work plane defined above this node in the geometry sequence. If you choose a work plane, the work plane and its coordinate system appear in the Graphics window, using an extra coordinate triad with the directions
xw,
yw, and
zw (which are then used to specify the control points’ location).
Select the Resulting objects selection check box to create predefined selections (for all levels — objects, domains, boundaries, edges, and points — that are applicable) in subsequent nodes in the geometry sequence. To also make all or one of the types of resulting entities (domains, boundaries, edges, and points) that the Bézier polygon consists of available as selections in all applicable selection lists (in physics and materials settings, for example), choose an option from the
Show in physics (
Show in instances if in a geometry part;
Show in 3D in a plane geometry under a work plane in a 3D component) list:
All levels,
Domain selection (2D only),
Boundary selection (2D only),
Edge selection (3D only), or
Point selection. The default is
Domain selection in 2D and
Edge selection in 3D. These selections do not appear as separate selection nodes in the model tree. Select
Off to not make any selection available outside of the geometry sequence. From the
Color list, choose a color for highlighting the resulting objects selection. See
Selection Colors.
are the Bernstein basis functions of
degree p;
bi = (x1, …,
xn) are the control points of the
n-dimensional space; and
wi are the weights, which should always be nonnegative numbers. The endpoint interpolation property corresponds to
b(0) = b0 and
b(1) = bp. Another useful property of the rational Bézier curves is that the direction of the tangent vector at
t = 0 and
t = 1 is determined by the vectors
b1 − b0 and
bp − bp−1, respectively. That is, the curve is always tangent to the line connecting the control points
b0 and
b1 and the line connecting
bp−1 and
bp. When joining curves at endpoints, aligning the (nonzero) tangent vectors assures tangential continuity. This technique produces visually smooth transitions between adjacent curves.
Rational Bézier curves of degree 2 can represent all conic sections: circles, ellipses, parabolas, and hyperbolas. Elliptical or circular curve segments are often called arcs. The conic sections are also called quadric curves or quadrics. Because the parameter
t is constrained to be in the interval
[0, 1], only a segment of the conic section is represented. A 2nd degree curve consists of three control points and three weights. There is a simple rule for classifying a 2nd degree curve if the endpoint weights are set to
1, only allowing the central weight
w1 to vary: if
w0 = w2 = 1, then
0 < w1 < 1 gives ellipses,
w1 = 1 gives parabolas, and
w1 > 1 gives hyperbolas. For a fixed control polygon,
at most one value of
w1 (among the ellipses generated by letting
0 < w1 < 1) gives a circle segment. For example, a quarter of a full circle is generated by a control polygon with a right angle and with a central weight of
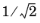
.