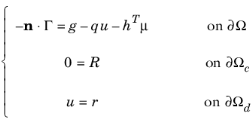The formulation of the boundary conditions in general form (Equation 16-1) and coefficient form (
Equation 16-2) imposes both Dirichlet and Neumann conditions at the same time:
where Γ is the
flux vector (
Γ = −c∇u−αu+γ for a coefficient form equation) and
δΩc and
δΩd are parts of the overall boundary,
δΩ, where general constraints and Dirichlet conditions have been specified. Combining conditions of different types on the same boundary is possible because of a new dependent variable
μ, which is defined only on the boundary. This unknown variable
μ is called a
Lagrange multiplier and usually has a physical interpretation. For example, in structural mechanics problems, the Lagrange multiplier equals the reaction forces on the boundary.
The factor hT in the Neumann boundary condition is the
constraint force Jacobian. It decides how the Lagrange multipliers enforcing the constraint are scaled and distributed over the equations. The default settings in a
Constraint node use
while a Dirichlet Boundary Condition node by default corresponds to
hT =
−1. For example:
The Lagrange multiplier, μ, adjusts so as to satisfy the requested Dirichlet condition. Specifying a nonzero
g changes the value of the Lagrange multiplier on the same boundary but does not affect the actual solution
u. Therefore, this equation can usually be ignored, leaving effectively a pure Dirichlet condition.
The following example demonstrates a number of possible boundary condition combinations for a stationary system with two dependent variables u1 and
u2 and two constraints when reaction terms are applied symmetrically on all physics. This is the default, and most useful, implementation. Written in general form:
Let R1 =
R2 =
0. Then the Dirichlet boundary conditions give
0 =
0. In addition, the terms containing the Lagrange multipliers disappear from the Neumann boundary condition. Thus you have only the Neumann boundary conditions:
Let R1 =
r1 − u1 and
R2 =
r2 − u2. Then the Dirichlet conditions are the usual
u1 =
r1 and
u2 =
r2. Using default settings for the constraint reaction terms,
These last equations impose no restrictions on u1 or
u2, because the Lagrange multipliers
μ1 and
μ2 always adjust so as to fulfill the Dirichlet conditions. In this case, ignore the Neumann boundary conditions.
Let R1 =
r1 − u1 and
R2 = 0. Then the Dirichlet conditions are
The first Neumann condition can be ignored because it imposes no restriction on u1 or
u2. You effectively have only the Dirichlet condition on
u1 together with the second Neumann condition.
The Dirichlet condition is similar to that in Case 3: u1 =
r1. By default, the Neumann conditions then become:
Effectively, you have only the Neumann condition −n ·
Γ1 = G1. In comparison with Case 3, the PDEs and the Dirichlet conditions are identical, while the Neumann conditions are different. Both the Dirichlet and the Neumann conditions are now applied on
u1, and nothing is specified for
u2.
Finally, let R1 =
u2 − u1 and
R2 = 0. Also, assume that
u1 and
u2 exist on two adjacent domains rather than on the same domain. The normal vectors as seen from the two sides are then
n1 = −n2 = n. Then the Dirichlet conditions are:
The same Lagrange multiplier now appears in both Neumann conditions, which can have different definitions of Γ and
G. Therefore, contrary to Cases 2 and 3, the Neumann conditions cannot be ignored. Instead, adding the two conditions, it becomes apparent that the solution and flux on the boundary must fulfill:
In particular, if G1 = G2 = 0, the last condition simplifies to:
This means that both the variables u1 and
u2 and the corresponding fluxes are equal at the boundary. If
u1 and
u2 represent the same quantity, this is the same continuity condition that holds implicitly at every mesh element boundary in the model, where nothing else has been specified.