Theory for the Large Eddy Simulation Interfaces
Large Eddy Simulations offer an alternative approach to turbulent flow simulations as compared to the RANS approach (see Theory for the Turbulent Flow Interfaces). In LES, the larger three-dimensional, unsteady eddies are resolved, whereas the effect of the smaller eddies is modeled. This requires the simulations to be three-dimensional and time dependent. The current implementation of the LES interfaces is suitable for incompressible flow only. The velocity and pressure fields are divided into resolved and unresolved scales. Denoting the fields containing all scales with capital letters, the decomposition can be expressed as,
(4-162)
Inserting Equation 4-162 into the incompressible form of the Navier-Stokes equation and the continuity equation yields,
(4-163)
Next, Equation 4-163 is projected onto the finite element sub-spaces of the resolved velocity and pressure scales. Denoting the test functions for these scales by v and q, respectively, the projection can be expressed as,
(4-164)
In Equation 4-164, f is the applied traction force on the boundary ∂Ω of the spatial domain Ω, and the stresses in the last term on the right-hand side are the resolved nonlinear advection term, the two cross-stresses, and the Reynolds stress. By assuming that the unresolved scales are orthogonal to the inner-product space of the resolved scales, the unresolved time derivative and viscous terms vanish. Another assumption made in the derivation of Equation 4-164 is that u' vanishes on ∂Ω (see Ref. 1 for further details).
In the Residual Based Variational Multiscale (RBVM) method, the unresolved velocity and pressure scales are modeled in terms of the equation residuals for the resolved scales,
(4-165)
where the momentum and continuity equation residuals are given by,
(4-166)
and the intrinsic time-scales are given by,
(4-167)
Here, C1 is a constant depending on the temporal scheme, C2 a constant depending on the shape of the element, and C3 a constant depending on both the order of the shape functions and the shape of the element. G is the covariant metric tensor. When the Use dynamic subgrid time scale option is selected, the first term under the square-root in Equation 4-167 is replaced by an estimate of the time-derivative based on the resolved scales.
In certain cases, the residual-based Reynolds-stress contribution has been found to be too small (see Ref. 2). For this reason, the Residual Based Variational Multiscale with Viscosity (RBVMWV) method adds a residual based viscosity term to the right-hand side of Equation 4-164,
(4-168)
where 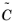is a model constant, and h is a measure of the element size.
For the Smagorinsky model, the Reynolds stress term is replaced by,
(4-169)
where,
(4-170)
and 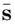is the projection of S onto the space of constant shape functions. This corresponds to a further decomposition of the resolved scales into large resolved scales and small resolved scales, in which only the latter are affected by the Reynolds stress (see Ref. 3).
Note that all three models require equal-order interpolation for velocity and pressure.
Furthermore, adequate resolution of wall-layers, , and convective time scales, , is essential in order to obtain accurate results in LES. Here, uτ is the friction velocity, hw the thickness of the first mesh-cell next to the wall, and hU the mesh size in the streamline direction.