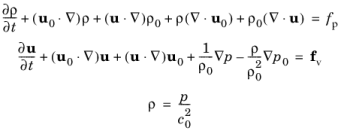The Convected Wave Equations node adds the equations for modeling the propagation of acoustic waves in a stationary background flow. Adiabatic behavior is assumed, meaning that this in some sense represents pressure acoustics in the presence of flow. The convected wave equation model solves the linearized Euler equations also referred to as linear acoustic equations for moving media. The equations are valid for any stationary background mean flow as long as there are not too large gradients in the background properties.

where u0 is the background mean flow velocity, p0 is the background mean flow pressure, ρ0 is the background mean flow density, and c0 is the speed of sound. All background properties can vary in space. The right-hand side sources fp and fv can be defined by the Domain Sources. More information about the governing equations is given in the Theory for the Convected Wave Equation Interface section.

In the Settings window, define the properties for the acoustics model and model inputs including the background mean flow, pressure, and velocity.

In order to model the influence the background mean flow has on the propagation of the acoustic waves in the fluid, the Background mean flow pressure p0 and Background mean flow velocity u0 need to be defined. If a material that is temperature dependent is used the Background mean flow temperature T0 field is also present.

All the background mean flow parameters can be functions of space. They can be either analytical expressions (user defined) or they can be picked up from a fluid flow simulation performed using the CFD Module. In this case use the Background Fluid Flow Coupling multiphysics feature to ensure correct mapping of the flow data. By default they are set to the quiescent constant background conditions of air.

Select a Fluid model either as Linear elastic (the default) or General dissipation. For both options define the background mean flow density ρ0 (SI unit: kg/m3) and the background mean flow speed of sound c0 (SI unit: m/s). The default is to use the property values from the material (From material). Select User defined from the list to enter a user-defined value in the text field that appears. For the General dissipation option also define the Sound diffusivity δ (SI unit: m2/s).

The density can also be picked up from a fluid flow simulation when the Background Fluid Flow Coupling multiphysics feature is used.

To display this section, click the Show More Options button () and select Stabilization in the Show More Options dialog box. In this section, you specify the value of the Lax-Friedrichs flux parameter τLF (default value: 0.2). This value controls the numerical flux between the elements (nodal discontinuous Lagrange elements) used with the discontinuous Galerkin (dG) method. The numerical flux defines how adjacent elements are connected and how continuous p and u are. Different definitions of the numerical flux lead to different variants of the dG method. The flux implemented here is the so-called global Lax-Friedrichs numerical flux. The value of the parameter τLF should be between 0 and 0.5. For τLF = 0 a so-called central flux is obtained. Setting τLF = 0.5 gives a maximally dissipative global Lax-Friedrichs flux.

To display this section, click the Show More Options button () and select Advanced Physics Options in the Show More Options dialog box. By default, the filter parameters α, ηc, and s are not active. Select the Activate check box to activate the filter. The filter provides higher-order smoothing for the dG formulation and can be used to stabilize the solution, for example, when a large background flow is present or large gradients are present. Inside absorbing layers the settings given here are overridden by the Filter Parameters for Absorbing Layers.

Enter values for the filter parameters in the corresponding text fields (default values: 36, 0.6, and 3). α must be positive and lie between 0 and 36. α = 0 means no dissipation and α = 36 means maximal dissipation. ηc should be between 0 and 1, where 0 means maximal filtering and 1 means no filtering (even if filtering is active). The s parameter should be larger than 0 and controls the order of the filtering (a dissipation operator of order 2s). For s = 1, you get a filter that is related to the classical 2nd-order Laplacian. A larger s gives a more pronounced low-pass filter.