Incident Pressure Field

The node is a subnode to all nonreflecting boundary conditions (plane, cylindrical, spherical wave radiation, and matched boundary). From the toolbar, add to Matched Boundary, Plane Wave Radiation, Spherical Wave Radiation, or Cylindrical Wave Radiation nodes. In the frequency domain, four options exist for the : , , , and .

The has built-in functionality to perform a plane wave expansion. This allows modeling scattering problems involving 2D axisymmetry using a 2D axisymmetric, model even though a plane wave is not in general axisymmetric.

	When calculating, for example, a transfer function, use the defined variable acpr.p_i for the incident field value on the boundary. This variable contains phase information that can be difficult to assess otherwise.

	When a perfectly matched layer (PML) is present in the model, do not apply incident fields on its outer boundaries. The PML is applied to absorb waves that move out of the computational domain. Defining an incident field on its boundary will lead to unphysical results.

From the list, select (the default), , , or to define the incident pressure field type.

If the incident pressure field pi is a predefined plane wave, it is of the type:

where p0 is the wave amplitude, k is the wave vector with amplitude ks = ω/c and wave direction vector ek, and x is the location on the boundary.

For enter a p0 (SI unit: Pa), the c (SI unit: m/s) of the medium defining the incident wave, the ek (SI unit: m), and a

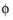
(SI unit: rad).

In 2D axisymmetric models, the incident fields take a slightly different form due to the geometrical restrictions. Only the z-component for the ek can be entered. Per default, the wave can only travel in the axial direction, since this is the only axisymmetric form of a plane wave.

By selecting , the plane wave is expanded in its cylindrical harmonics and a general ek can be selected. This sets up a wave of the form:

where m is the specified in the Pressure Acoustics Equation Settings. To expand the solution, it is necessary to run a over the mode number from 0 up to the desired resolution.

If the incident pressure field pi is a predefined cylindrical wave, it is of the type:

where p0 is the amplitude given at the reference distance rref = 0.548/ks (the distance where the Hankel function is one), ks = ω/c is the wave number,

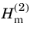
is the Hankel function of the second kind (representing an outgoing cylindrical wave), rs is the distance from the source axis, esa is the direction of the source axis, x0 is a point on the source axis, and x is the location on the boundary.

For , enter a p0 (SI unit: Pa), the c (SI unit: m/s) of the medium defining the incident wave, a x0 (SI unit: m), a esa (the vector is automatically normalized), and a

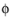
(SI unit: rad).

In 2D axisymmetric models, the incident fields take a slightly different form due to the geometrical restrictions. No source location nor axis is needed, as the source is always located on the z-axis.

If the incident pressure field pi is a predefined spherical wave (only for 2D axisymmetric and 3D), it is of the type:

where p0 is the amplitude given at the reference distance of 1 m, ks = ω/c is the wave number, rs is the distance from the source, x0 is the source location of the spherical wave, and x is the location on the boundary.

For , enter a p0 (SI unit: Pa), the c (SI unit: m/s) of the medium defining the incident wave, a x0 (SI unit: m), and a

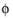
(SI unit: rad).

In 2D axisymmetric models, the incident fields take a slightly different form due to the geometrical restrictions. Only enter the z-coordinate for the z0 (SI unit: m) since the source is always located on the z-axis in a 2D axisymmetric model.

	For both the cylindrical and the spherical wave options, the source and/or source axis should be located outside the computational domain where the radiation condition is applied. The fields should be incident on the radiation boundary.

If is selected, enter the expression for the pi (SI unit: Pa) as a function of space.