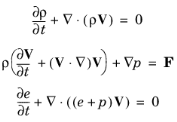Consider a compressible and inviscid fluid in some domain Ω. The motion and state of the fluid is described by its velocity V, density ρ, pressure p, and total energy per unit volume e. Its dynamics is governed by the Euler equations, expressing the conservation of mass, momentum, and energy (see General Governing Equations):

Here a volume force F has been included on the right-hand side of the momentum equation, whereas a possible heat-source term on the right-hand side of the energy equation (the last one) has been set to zero.

where γ = Cp /CV is the ratio of specific heats, Cp is the specific heat at constant pressure and CV at constant volume, while pref and ρref are reference quantities for the pressure and the density, respectively. An alternative form of the ideal-fluid state equation is

The assumption that the fluid is barotropic means that p = p(ρ). Taking the total time derivative and using the chain rule, leads to the relation

Assuming the flow to be irrotational, there exists a velocity potential field Φ, such that V = ∇Φ. If, in addition, the volume force is assumed to be given by F = −ρ∇Ψ, where Ψ is referred to as the force potential, the second of Equation 5-13 can be integrated to yield the Bernoulli equation

In this equation, two additional reference quantities have entered: the velocity vref, and the force potential Ψref, both valid at the same reference point as pref and ρref. Note, in particular, that neither the pressure p, nor the energy per unit volume e, appears in this equation.

where γ is the ratio of specif heats and Ψ denotes a possible domain force potential (SI unit: J/kg). In this equation, subscript ref signifies reference quantities that apply at a specific point or surface. Thus, pref is a reference pressure, ρref is a reference density, vref is a reference velocity, and Ψref is a reference force potential.