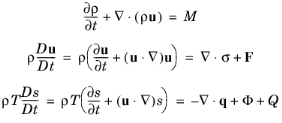where u is the velocity field,
ρ is the density,
T is the temperature,
s is the specific entropy,
σ is the stress tensor,
q is the local heat flux,
Φ is the viscous dissipation function, and
M,
F, and
Q are source terms. The operator
D/Dt is the material derivative (or advection operator) defined as
Some thermodynamic relations are necessary when reformulating the energy equations in terms of other sets of thermodynamic variables, like (p,
T) or (
ρ,
p). They are the density differential, the specific energy relation, a relation due to Helmholtz, and the fundamental entropy relation:
where u is the specific internal energy,
αp is the coefficient of thermal expansion (isobaric), and
βT is the isothermal compressibility. See, for example,
Ref. 5 and
Ref. 6 for details. They are defined together with the specific heat at constant pressure
Cp and specific heat at constant volume
Cv as
where k is the thermal conduction,
μ is the dynamic viscosity, and
μB is the bulk viscosity. This then also defines the viscous dissipation function
In the following, the governing equations are linearized and expanded to first order in the small parameters around the average stationary background solution. For details about perturbation theory see Ref. 3,
Ref. 4, and
Ref. 8. The small parameter variables (1’st order) represent the acoustic variations on top of the stationary background mean (or average) flow (0’th order solution). Note that, when solving the equations, the value of the acoustic field variables can also represent nonacoustic waves like thermal waves (entropy waves) and vorticity waves. In the time domain, these can be linear instabilities and can actually represent the onset of turbulence.
where A is any of the dependent variables or sources. In the frequency domain, the first order variables are assumed to be harmonic and expanded into Fourier components, such that
The first order variation to material parameters, that are not treated as dependent variables like the density ρ in the Linearized Navier-Stokes interface, is expressed using the density differential and related to perturbations in the temperature and the pressure.