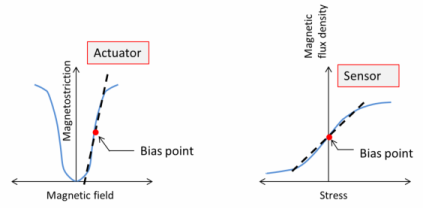
Magnetostrictive Material

Magnetostriction describes the change in dimensions of a material due to a change in its magnetization. This phenomenon is a manifestation of magnetoelastic coupling, which is exhibited by all magnetic materials to some extent. The effects related to magnetoelastic coupling are described by various names. The Joule effect describes the change in length due to a change in the magnetization state of the material. This magnetostrictive effect is used in transducers for applications in sonars, acoustic devices, active vibration control, position control, and fuel injection systems.

The inverse effect accounts for the change in magnetization due to mechanical stress in the material. This effect is also known Villari effect. This effect is mostly useful in sensors.

Magnetostriction has a quantum-mechanical origin. The magneto-mechanical coupling takes place at the atomic level due to spin-orbit coupling. From a system level, the material can be assumed to consist of a number of tiny ellipsoidal magnets which rotate due to the torque produced by the externally applied magnetic field. The rotation of these elemental magnets produces a dimensional change leading to free strain in the material.

The magnetostriction has a nonlinear dependence on the magnetic field and the mechanical stress in the material. However, the effect can be modeled using linear coupled constitutive equations if the response of the material consists of small deviations around an operating point (bias point).

It is possible to express the relation between the stress S, strain ε, magnetic field H, and magnetic flux density B in either a stress-magnetization form or strain-magnetization form:

where μ0 is the magnetic permeability of free space, cH and sH are respectively the stiffness and compliance matrices measured at constant magnetic field, and μrS and μrT are the relative magnetic permeabilities measured at constant strain and constant stress, respectively. The matrices dHT and eHS are called piezomagnetic coupling matrices.

In COMSOL Multiphysics, both constitutive forms can be used; simply select one, and the software makes all necessary transformations. The following equations transform strain-magnetization material data to stress-magnetization data:

You find all the necessary material data inputs within the Magnetostrictive Material node under the Solid Mechanics interface, which are added automatically when you add a predefined Magnetostriction multiphysics interface. Such a node can be also added manually under any Solid Mechanics interface similar to all other material model features. The Magnetostrictive Material uses Voigt notation for the anisotropic material data. More details about the data ordering can be found in Orthotropic and Anisotropic Materials section.

For a crystalline material with tetragonal symmetry, the strain-magnetization form of the constitutive relations is the following:

The following material data corresponds to Terfenol-D at 100 kA/m bias and 30 MPa prestress (Ref. 5):

A commonly accepted micromagnetic description of the magnetostriction is as follows (Ref. 2):

All domains have magnetization of the same magnitude |M| = Ms, but the magnetization can have different orientations characterized by the corresponding direction vector m = M/Ms for each domain. The applied magnetic field changes the domain orientation.

	In this section, the term domain refers to a small part of magnetic material. This is typical for micromagnetics literature, and it should not be mistaken with the concept of domain as part of the model geometry, the latter is often used in COMSOL Multiphysics documentation.

For a single crystal with cubic symmetry, the magnetostrictive strain tensor can be written as the following quadratic form:

where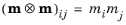

. Note that the magnetostrictive strain is represented by a deviatoric tensor, that is, tr(εme) = 0. This is because the deformation is related to the magnetic domain rotation, and such process should not change the material volume.

The strain in any direction given by the directional cosines βi can be written as

	The notation lambda is used for strain in this section, which is typical for micromagnetics literature. This should not be mistaken with the same notation used for stretch in other parts of the theory in COMSOL Multiphysics documentation.

Using Equation 3-54, one gets

When both magnetization and measurement direction are parallel to the same crystal direction [100], one has m1 = β1 = 1 and all other components are zero, so that

and λ = λ111.

If the strain is measured in [100] direction, while all the magnetization vectors are aligned perpendicular to it, one has only the following two nonzero components: m2 = β1 = 1 and consequently:

In many applications, such alignment of the domains is achieved by applying a compressive prestress. Thus, the maximum usable magnetostriction is achieved via a 90-degree rotation of the domains

For an isotropic material, λ100 = λ111 = λs, and Equation 3-54 becomes

For a polycrystalline material without preferred orientation, the following approximation can be used (Ref. 1):

In COMSOL Multiphysics, this description of the magnetostriction is modeled using the following equation for the magnetostrictive strain:

The strain field is deviatoric, and Equation 3-56 exhibits the same properties as Equation 3-54 at saturation, that is, when |M| → Ms. Equation 3-55 is replaced by

Note that the strain vanishes when |M| → 0, which makes the model applicable in the whole range from full demagnetization to saturation.

For isotropic materials, the magnetostrictive strain is modeled as the following quadratic isotropic form of the magnetization field (Ref. 3):

The stress in the magnetostrictive material is modeled as

For isotropic materials, the stiffness matrix cH can be represented in terms of two parameters, for example, using the Young’s modulus and Poisson’s ration. Cubic materials possess only three independent components: c11, c12, and c44.

Using Equation 3-57, one can derive a linear response around a given bias state characterized by a premagnetization vector M0. Thus,

where M1 is a perturbation, and

If one assumes a unidirectional state, for example

it will further simplify into

Nonlinear magnetization in the magnetostrictive material is found from the following nonlinear implicit relation (Ref. 4):

where L is the Langevin function

with χm being the magnetic susceptibility in the initial linear region.

Other possible choices of the L function are a hyperbolic tangent

and a linear function

The latter option will make it possible to find an explicit expression for the magnetization. However, such model does not have a proper saturation behavior, and thus it should be used only in the operating range far from saturation. Both the Langevin function and hyperbolic tangent models requires the magnetization vector components to be treated as extra dependent variables.

For cubic crystals, the effective field in the material is given by

where H is the applied magnetic field. The second term in Equation 3-58 represents the mechanical stress contribution to the effective magnetic field, and thus to the material magnetization, which is called the Villari effect. The deviatoric stress tensor is related to the strain as

For isotropic materials, the effective magnetic field expression simplifies into

In addition, the magnetization and magnetic field are related to each other and to the magnetic flux density (also called the B-field) by

COMSOL Multiphysics solves for the magnetic vector potential A whose curl yields the vector B-field. The H-field is then obtained as a function of the B-field and magnetization.