The Bresler-Pister criterion (Ref. 2, Ref. 17) was originally devised to predict the strength of concrete under multiaxial stresses. This failure criterion is an extension of the Drucker-Prager Criterion to brittle materials, and it can be expressed in terms of the stress invariants as

here, k1, k2, and k3 are parameters obtained from the uniaxial compressive strength σc, the uniaxial tensile strength σb, and the biaxial compressive strength σb

All the strengths are considered with a positive sign. Note that for typical strength values, the parameters k1 and k2 are positive while k3 is negative.

The Willam-Warnke criterion (Ref. 10) is used to predict failure in concrete and other cohesive-frictional materials such as rock, soil, and ceramics. Just as the Bresler-Pister Criterion, it depends only on three parameters. It was developed to describe initial concrete failure under triaxial conditions. The failure surface is convex, continuously differentiable, and it is fitted to test data in the low compression range.

where σc is the uniaxial compressive strength, σt is uniaxial tensile strength, and σb is the biaxial compressive strength (all parameters are positive). The octahedral normal and shear stresses are defined as usual; see Other Stress Invariants

so the criterion in Equation 3-39 can be written in term of stress invariants as

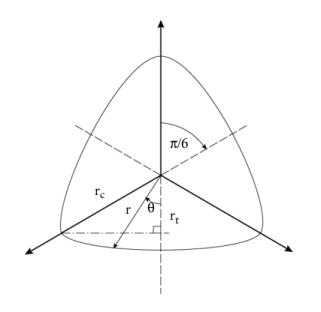
The dimensionless function r(θ) describes the segment of an ellipse on the octahedral plane as a function of the Lode angle θ

Here, the tensile and compressive meridian rt and rc are defined in terms of the strengths σc, σb, and σt:

The function r(θ) can be interpreted as the friction angle which depends on the Lode angle θ (Ref. 10).

The Ottosen criterion is a four-parameter failure criterion proposed for short-time loading of concrete. It corresponds to a smooth convex failure surface with curved meridians, which is open in the negative (compressive) direction of the hydrostatic axis. The curve in the pi-plane changes from almost triangular to a more circular shape with increasing hydrostatic pressure. The criterion agrees with experimental results over a wide range of stress states, including both triaxial tests along the tensile and the compressive meridian and biaxial tests (Ref. 18).

The Ottosen criterion is commonly written as (Ref. 17, Ref. 18):

Here, σc > 0 is the uniaxial compressive strength of concrete, and a>0 and b>0 are dimensionless parameters. The dimensionless function λ(θ) depends on the Lode angle θ and the dimensionless parameters k1 > 0 and k2 > 0.

The parameter k1 is called the size factor. The parameter k2 (also called shape factor) is positive and bounded to 0 ≤ k2 ≤ 1(Ref. 17, Ref. 18).

Typical values for these parameters are obtained by curve-fitting the uniaxial compressive strength σc, uniaxial tensile strength σt, and from the biaxial and triaxial data (for instance, a typical biaxial compressive strength of concrete is 16% higher than the uniaxial compressive strength). The parameters σc, σb, and σt are positive.

The compressive and tensile meridians (as defined in the Willam-Warnke Criterion) are

The Hoek-Brown criterion is an empirical type of model which is commonly used when dealing with rock masses of variable quality. The Hoek-Brown criterion is widely used within civil engineering and is popular because the material parameters can be estimated based on simple field observations together with knowledge of the uniaxial compressive strength of the intact rock material. The Hoek–Brown criterion is one of the few nonlinear criteria widely accepted and used by engineers to estimate the yield and failure of rock masses. The original Hoek-Brown failure criterion states (Ref. 5)

where σ1 ≥ σ2 ≥ σ3 ≥ 0 are the principal stresses at failure (as defined in geotechnical engineering; that is, an absolute value), σc is the uniaxial compressive strength of the intact rock (positive parameter), and m and s are positive material parameters.

with σc, m, and s positive material parameters. (In this case, note that σ1 <  sσc/m).

As developed originally, there is no relation between the parameters m and s and the physical characteristics of a rock mass measured in laboratory tests. However, for intact rock, s = 1 and m = mi, which is measured in a triaxial test.

For jointed rock masses, 0 ≤ s < 1 and m < mi. The parameter m usually lies in the range 5 < m < 30 (Ref. 7).

The Hoek-Brown criterion can be written in terms of the invariants I1 and J2 and the Lode angle 0 ≤ θ ≤ π/3, so

The generalized Hoek-Brown criterion was developed in order to fit the Geological Strength Index (GSI) classification of isotropic rock masses (Ref. 6). A new relationship between GSI, m, s and the newly introduced parameter a was developed, to give a smoother transition between very poor quality rock masses (GSI < 25) and stronger rocks

In terms of the invariants J2 and the Lode angle this equals

where σ1 ≥ σ2 ≥ σ3 are the principal stresses (using the Structural Mechanics Module conventions) of the effective stress tensor (this is, the stress tensor minus the fluid pore pressure).

The positive parameter mb is a reduced value of the material constant mi:

s and a are positive parameters for the rock mass given by the following relationships:

The disturbance factor D was introduced to account for the effects of stress relaxation and blast damage, and it varies from 0 for undisturbed in situ rock masses to 1 for very damaged rock masses.