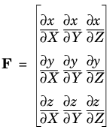The heat equation can be formulated either in a spatial coordinate system, with coordinate axes fixed in space, or in a
material coordinate system, fixed to the material in its reference configuration and following the material as it deforms. COMSOL Multiphysics refers to these coordinate systems as the
spatial frame and the
material frame. In the case of immobile and undeformed materials, these two frames coincide.
The spatial frame is well adapted to simulate heat transfer in liquids and gases, where it is unreasonable to follow the state of individual material particles. The temperature is computed at fixed positions in space.
In solids, the material frame is more convenient. The temperature is computed at material particles uniquely identified by their position in some given reference configuration. It makes in particular the anisotropic material properties (thermal conductivity for example) independent of the current spatial orientation of the material.
The position vector in the physical space is identified by the lowercase symbol x and lowercase letters
x,
y, and
z for each coordinate (or
r,
ϕ, and
z in axisymmetric components). After a given transformation, the position of an elementary volume is modified in the spatial frame but not in the material frame. The position vector in the this material frame is denoted by the uppercase symbol
X and uppercase letters
X,
Y, and
Z for each coordinate (or
R,
Φ, and
Z in axisymmetric components).
It relates elementary distances dx and
dX in the domain, expressed in material and spatial frames, according to:
The determinant of the deformation gradient, det(F), is the
volume ratio field. In COMSOL Multiphysics,
det(F) should always be strictly positive. Otherwise, the negative value is likely to be caused by an inverted mesh during the resolution of the model since it corresponds to a mathematical reflection operation.