Modeling Layered Materials

The Heat Transfer interfaces contain several lumped conditions for modeling heat transfer in layered materials: Thin Layer, Thin Film, Fracture, and Thin Rod.

In addition, standalone physics interface are available for the modeling of heat transfer by conduction, convection and radiation in thin structures:

•

The Heat Transfer in Shells Interface

•

The Heat Transfer in Films Interface

•

The Heat Transfer in Fractures Interface

Either the Thin Layer (Heat Transfer interface) and Solid (Heat Transfer in Shells interface), Thin Film (Heat Transfer interface) and Fluid (Heat Transfer in Shells interface), or Fracture (Heat Transfer interface) and Porous Medium (Heat Transfer in Shells interface) feature is available by default in each of these interfaces.

The features mentioned above are the counterparts of domain features for the modeling of heat transfer in solid, fluid, and porous thin structures that can be represented as boundaries or edges, as described in Table 4-2.

Table 4-2: Equivalent domain and thin structures features
Type of Medium	Domain Feature	Boundary Feature	Edge Feature
Solid	Solid	Thin Layer (ht) Solid (htlsh)	Thin Rod (ht)
Fluid	Fluid	Thin Film (ht) Fluid (htlsh)	—
Porous	Porous Medium	Fracture (ht) Porous Medium (htlsh)	—

All these functionalities have in common the fact that the thin domains they model are lumped into boundaries (for Thin Layer, Thin Film and Fracture) or 3D edges (for Thin Rod).

Reduced Mesh Element Number

A significant benefit is that a thin structure can be represented as a boundary instead of a domain and a rod can be represented as a 3D edge. This simplifies the geometry and reduces the required number of mesh elements. Figure 4-3 shows an example where a thin structure significantly reduces the mesh density.

Figure 4-3: Modeling a copper wire as a domain (top) requires a denser mesh compared to modeling it as a boundary with a conductive layer (bottom).

Thin structure as an Extra Dimension

To model heat transfer through the thickness of a thin structure, or multiple sandwiched layers with different material properties and thicknesses, COMSOL Multiphysics gives the possibility to create a product space between the dimensions of the boundary and an additional dimension. This is realized by the Extra Dimension tool through either the option of the Thin Layer (Heat Transfer interface) and Solid (Heat Transfer in Shells interface), Thin Film (Heat Transfer interface) and Fluid (Heat Transfer in Shells interface), or Fracture (Heat Transfer interface) and Porous Medium (Heat Transfer in Shells interface) features.


	Adding Extra Dimensions to a Model and Using Extra Dimensions in the COMSOL Multiphysics Reference Manual. Plotting Results in Thin Layers Extra Dimensions

An additional 1D segmented line represents the thickness of the thin structure. The number of mesh points for each interval of the extra dimension is set to 2 by default.

Tangential and Normal Gradients

In thin structures, the tangential gradient and the normal gradient can be more appropriate to express the governing equations.

The normal gradient is the projection of the gradient operator onto the normal vector, n, of the boundary representing the thin structure. This is mathematically expressed for any scalar field T as:

The tangential gradient removes the normal component from the gradient operation, so that only tangential components remain. This is mathematically expressed for any scalar field T as:

The gradient operator is then split into a tangential part and a normal part:

(4-36)

This relation simplifies to:

when tangential heat transfer is dominant or negligible. These results will be useful in the next sections describing heat transfer in the different thin structures.


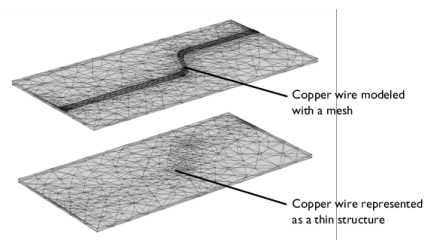
	It should be noted that when an extra dimension is used, the equations are written from the point of view of the extra dimension. In particular, the dtang() operator would correspond to ∇n since it performs the derivation along the extra line. In the thin structure boundary, dtang() would correspond to ∇t.

Thermal Conductivity Tensor in Local Boundary Systems

The thermal conductivity k describes the relationship between the heat flux vector q and the temperature gradient ∇T as in

which is Fourier’s law of heat conduction (see also The Physical Mechanisms under Heat Transfer).

The tensor components can be specified in the local coordinate system of the boundary, which is defined from the geometric tangent and normal vectors. The local x-direction, ex, loc, is the surface tangent vector t1, and the local z-direction, ez, loc, is the normal vector n. Their cross product defines the third orthogonal direction such that:

From this, a transformation matrix between the local coordinate system and the global coordinate system can be constructed in the following way:

The thermal conductivity tensor in the local coordinate system, kbnd, is then expressed as