A stationary formulation has per definition no time derivatives and Equation 3-17 reduces to:

Solving Equation 3-56 requires a starting guess that is close enough to the final solution. If no such guess is at hand, the fully transient problem can be solved instead. This is, however, a rather costly approach in terms of computational time. An intermediate approach is to add a fictitious time derivative to Equation 3-56:

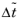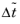
where is a pseudo time step. Since u−nojac(u) is always zero, this term does not affect the final solution. It does, however, affect the discrete equation system and effectively transforms a nonlinear iteration into a step of size of a time-dependent solver.

where h is the mesh cell size. A small CFL number means a small time step. It is practical to start with a small CFL number and gradually increase it as the solution approaches steady state.

If the automatic expression for CFLloc is set to the built-in variable CFLCMP, then the automatic setting suggests a PID regulator for the pseudo time step in the default solver. The PID regulator starts with a small CFL number and increases CFLloc as the solution comes closer to convergence.

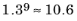
The variable niterCMP is the nonlinear iteration number. It is equal to one for the first nonlinear iteration. CFLloc starts at 1.3 and increases by 30% each iteration until it reaches . It remains there until iteration number 20 at which it starts to increase until it reaches approximately 106. A final increase after iteration number 40 then takes it to 1060. Equation 3-57 can, for some advanced flows, increase CFLloc too slowly or too quickly. CFLloc can then be tuned for the specific application.