The following background information about the Stationary Solver discusses these topics: Damped Newton Methods, Termination Criterion for the Fully Coupled and Segregated Attribute Nodes, Linear Solvers versus Nonlinear Solvers, and Pseudo Time Stepping. Also see Selecting a Stationary, Time-Dependent, or Eigenvalue Solver.

The nonlinear solver uses an affine invariant form of the damped Newton method as described in Ref. 3. You can write the discrete form of the equations as f(U) = 0, where f(U) is the residual vector and U is the solution vector. Starting with the initial guess U0, the software forms the linearized model using U0 as the linearization point. It solves the discretized form of the linearized model f'(U0) δU = −f(U0) for the Newton step δU using the selected linear system solver (f'(U0) is the Jacobian matrix). It then computes the new iteration U1 = U0 + λ δU, where λ (0 ≤ λ ≤ 1) is the damping factor. Next the modified Newton correction estimates the error E for the new iteration U1 by solving f'(U0) E = −f(U1). If the relative error corresponding to E is larger than the relative error in the previous iteration, the algorithm reduces the damping factor λ and recomputes U1. This algorithm repeats the damping-factor reduction until the relative error is less than in the previous iteration or until the damping factor underflows the minimum damping factor. When it has taken a successful step U1, the algorithm proceeds with the next Newton iteration.

A value of λ = 1 results in Newton’s method, which converges quadratically if the initial guess U0 is sufficiently close to a solution. In order to enlarge the domain of attraction, the solver chooses the damping factors judiciously. Nevertheless, the success of a nonlinear solver depends heavily on a carefully selected initial guess, so you should provide the best value for U0, giving at least an order of magnitude guess for different solution components.

You specify the termination criteria in the Settings window for a Fully Coupled or Segregated subnode to the Stationary Solver node. Also see The Segregated Solver (Termination Criterion for a Segregated Solver).

For Termination criterion: Solution, the nonlinear iterations terminate when the following convergence criterion is satisfied: Let U be the current approximation to the true solution vector, and let E be the estimated error in this vector. The software stops the iterations when the relative tolerance exceeds the relative error computed as the following weighted Euclidean norm:

Here M is the number of fields; Nj is the number of degrees of freedom in field j. The double subscript denotes degree of freedom index (i) and field (j) component. Let Wi,j = max(|Ui,j|, Sj), where Sj is a scale factor that the solver determines from the scaling method. You select the scaling method from the Method list in the Scaling section of the Dependent Variables node’s Settings window. The solver then computes the scale factor Sj using the following rules:

For Termination criterion: Residual, the nonlinear iterations terminate when the following convergence criterion is satisfied: The software stops the iterations when the relative tolerance exceeds the relative error computed as the weighted Euclidean norm

where F is the current residual. The weights are determined considering both the initial residual f0 and the residual after the first iteration f1 as f = 0.5 | f0| + 0.5 |  f1|. In the equation above, the double subscript denotes the degree of freedom index (i) and the field (j) component. The iterations can also terminate if the relative step size is in the range of a hundred machine epsilon and in addition a full Newton step is taken.

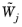
You select the scaling method from the Method list in the Residual Scaling section of the Dependent Variables node’s Settings window. The solver then computes the weights using the following rules:

For Termination criterion: Solution or residual, the nonlinear iterations terminate when the relative tolerance exceeds the relative error computed as the minimum of the solution-based error and the error given by the Residual factor times the residual-based error above.

For Termination criterion: Solution and residual, the nonlinear iterations terminate the Newton iterations on a solution-based estimated relative error and a residual-based estimated relative error given by the Residual factor times the residual-based error above.

where the controller parameters kP, kI, and kD for the proportional, integral, and derivative parts, respectively, are positive constants. Here en is the nonlinear error estimate for step n and tol is a given target error estimate.

After each segregated solver iteration, the log reports the Pseudo time-stepping CFL-ratio defined as min(log(CFL)/log(CFL∞),1.0), where CFL∞= 104 is the steady-state CFL number. The CFL ratio concerns the overall progress of the segregated solver and not individual groups. Convergence is allowed when this number is one and the usual convergence criteria are met.

Pseudo time stepping is available for stationary problems. In the coupled approach, it functions together with the constant damped Newton solver. See the settings for Fully Coupled and Segregated for related parameters.