Theory for Specific Current Distribution Feature Nodes
Electrolyte Theory
The Electrolyte node defines a current balance in the electrolyte. The domain equation is:
where il denotes the current density vector. In free electrolyte, there is no source or sink of charge.
The definition of the current density vector depends on the equation formulation of the electrolyte charge transport, as discussed above in Domain Equations for Primary and Secondary Current Distributions and Domain Equations for Tertiary Current Distributions Using the Nernst-Planck Equations and Electroneutrality.
•
For the Primary and Secondary Current Distribution interfaces, see Electrolyte.
•
For the Tertiary Current Distribution, Nernst-Planck interface, see Electrolyte.
Porous Electrode Theory
A porous electrode is a mixed material with one electrode phase and one electrolyte phase. (A special case of a porous electrode is the gas diffusion electrode, as found in a fuel cell. These contain a gas pore phase which is inert to charge transfer.) To model a porous electrode we define two separate current balances according to the following equations:
and
In these equations, il denotes the current density vector in the electrolyte, as discussed above in Domain Equations for Primary and Secondary Current Distributions and Domain Equations for Tertiary Current Distributions Using the Nernst-Planck Equations and Electroneutrality.
In addition to the current balances, it is necessary to also formulate mass balance equations for the species in the electrolyte phase for the tertiary case.
It is also common to used corrected conductivities and diffusion parameter values in a porous electrode to account for the lowered volume fraction of the conducting phase, and the longer transport distance due to the tortuosity of the pores.
The current balances in the pore electrolyte and in the electrode matrix contain sources and sinks according to the charge transfer reactions that take place in the electrode catalyst. For example, if only one charge transfer reaction takes place in the porous electrode and the rate of this reaction is described by the Butler-Volmer equation, the domain equations are the following:
where Av denotes the specific surface area (dimension L2/L3), and η the overpotential according to
and Eeq denotes the equilibrium potential for the charge transfer reaction.
If the porous electrode is a cathode, then the charge transfer reaction is a source for the current balance in the electrode, because it receives current from the pore electrolyte. The charge transfer reaction is then a sink for the current balance in the pore electrolyte, because the current is transferred from the pore electrolyte to the electrode in a cathodic reaction.
The corresponding sources and sinks in the current balances that are due to the charge transfer reactions are also coupled to the material balances for the charged species. This means that the exemplar Butler-Volmer expression above is also included in the material balances as a reaction term, Ri, by using Faraday’s laws for each of the species that take part in charge transfer reactions.
•
For the Primary and Secondary Current Distribution interfaces, see Porous Electrode.
•
For the Tertiary Current Distribution, Nernst-Planck interface, see Porous Electrode.
Electrode Reactions Theory
Charge transfer reactions occurring at an interface between an electrode and an electrolyte domain gives rise to a normal current flux that equals the sum of all reaction currents according to
where iloc,m (A/m2) is the Electrode Reaction current density of the charge transfer electrode reaction of index m, il the current density vector in the electrolyte and is the current density vector in the electrode.
Porous Electrode Reactions Theory
For a porous electrode, the electrode reaction current densities are multiplied by the surface area to yield a source or sink in the current balance domain equation according to:
where Av is the specific surface area of the electrocatalyst.
Porous Electrode Reaction
Electrode Theory
Electron conduction in an Electrode is modeled using Ohm’s law. The domain equation is the following:
where is denotes the current density vector according to:
and where σs denotes the electrical conductivity and 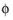s the electrolyte potential.
Electrolyte Current Density Theory
An applied current density can be defined as its component perpendicular to the boundary according to:
The current density can also be defined including all its components:
where il, bnd is a given expression for the current density vector.
Electrolyte Current Density
Electrolyte Current Theory
The Electrode Current boundary condition sets the total current at a given position in the electrolyte without imposing a current density distribution. The conditions yields a constant electrolyte potential, along the given boundary, that satisfies the total value of the current. The boundary condition is a good choice in the middle of a cell with planar electrodes, where the isopotential level can be a plane (or close to a plane in 3D, or line in 2D) but where the current density distribution is unknown.
The feature adds one unknown variable, the electrolyte potential, 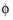l, bnd, along the boundary. It then adds one additional equation for the total current, which is an integral over the boundary:
The average current density condition imposes the same equation but multiplies the current density by the area of the boundary to obtain the value of the total current In, l.
Electrode Current Theory
The Electrode Current adds one unknown variable, the electric potential, s, bnd, along the boundary. It then adds one additional equation for the total current, which is an integral over the boundary:
where
and σs denotes the electrode conductivity and 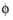s the electric potential. The average current density condition imposes the same equation but multiplies the current density by the area of the boundary to obtain the value of the total current, In,s.
Symmetry Theory
The Symmetry boundary condition, in the Primary Current Distribution and Secondary Current Distribution interfaces is identical to the Insulation condition and is expressed according to the equation below.
where ik denotes the current density vector and k = l, s is an index for the electrolyte and electrode, respectively.
The Symmetry boundary condition for the Tertiary Current Distribution, Nernst-Planck interface imposes a no-flux condition for the molar flux of species at a boundary. The condition is expressed as follows:
Electrode Current Density Theory
An applied Electrode Current Density can be defined as its component perpendicular to the boundary according to:
where
and σs denotes the electrode conductivity and 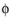s the electric potential.
The current density can also be defined including all its components:
where is, bnd is a given expression for the current density vector.
Electrode Power Theory
The Electrode Power boundary condition is used to specify either the total electrode power or the average electrode power density drawn from or inserted into an electrochemical cell at an electrode boundary.
For a total power condition, the boundary electric potential of an electrode is set to a potential s, bnd, defined by the condition for the total power on the boundary ∂Ω according to:
where 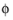s, ground is the ground potential of the cell, and Ptotal (W) is the power to be drawn.
For an average power condition, Ptotal is calculated by:
where Pavg is the average power density on the boundary, and A is the boundary area.
For a galvanic cell, such as a battery during discharge or a fuel cell, there is a maximum power level, beyond which a further current increase causes a lowered output power due to increasing voltage losses. A result of this is that there can be two existing solutions for the same power setting. In these cases the choice of initial values determines the final solution.
Electrode Power
Ion Exchange Membrane Theory
Ion-exchange membranes typically contain a polymer matrix with a number of fixed ionic groups.
Since these charges are fixed, there is no need to explicitly model the transport of these charges, but when calculating the sum of charges, used in the Nernst-Planck (with electroneutrality) or the Nernst-Planck-Poisson set of equations, one need to add this fixed space charge.
For Nernst Planck with electroneutrality, the electroneutrality condition reads
For the Nernst-Planck-Poisson case, the total space charge density becomes
Ion Exchange Membrane Boundary Theory
The electrochemical potential μi of a charged species of index i is
where T(K) is the temperature, R (mol/(J K)) the molar gas constant, ai is the species activity, 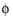l is the electrolyte potential, zi the species charge and F(C/mol) is Faraday's constant.
At equilibrium the electrochemical potentials on each side of the free electrolyte - ion-exchange membrane interface are equal.
Setting the species activity to equal the concentration and denoting the liquid electrolyte phase and a ion-exchange membrane phases as 1 and 2, respectively, the Donnan potential, (V), describes the relation between the concentration of a species, ci (mol/m3), at each side of the boundary and the electrolyte potentials:
which may be rearranged to
The molar flux of each species in the liquid electrolyte is continuous over the membrane-liquid interface
Since the total current density is the sum of all species fluxes, times the individual species charges, the current densities Il in the normal direction n of the membrane-liquid interface boundary is also continuous: