Wave propagation is modeled by equations from linearized fluid dynamics (pressure waves) and structural dynamics (elastic waves). The full equations are time dependent, but noting that a harmonic excitation of the field u has a time dependence of the form

gives rise to an equally harmonic response with the same frequency; the time can be eliminated completely from the equations. Instead the angular frequency ω = 2πf, enters as a parameter where f is the frequency. In COMSOL the +iω convection is used for the time harmonic formulations.

This procedure is often referred to as working in the frequency domain or Fourier domain as opposed to the time domain. From the mathematical point of view, the time-harmonic equation is a Fourier transform of the original time-dependent equations and its solution as function of ω is the Fourier transform of a full transient solution. It is therefore possible to synthesize a time-dependent solution from a frequency-domain simulation by applying an inverse Fourier transform.

The result of a frequency domain analysis is a complex time-dependent field u, which can be interpreted as an amplitude uamp = abs(u) and a phase angle uphase = arg(u). The actual displacement at any point in time is the real part of the solution:

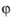
Visualize the amplitudes and phases as well as the solution at a specific angle (time). When using the Solution data sets, the solution at angle (phase) parameter makes this task easy. When plotting the solution, COMSOL Multiphysics multiplies it by eiϕ, where is the angle in radians that corresponds to the angle (specified in degrees) in the Solution at angle field. The plot shows the real part of the evaluated expression:

The angle 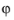is available as the variable phase (in radians) and is allowed in plot expressions. Both the frequency freq and angular frequency omega are available variables.