Although boundary conditions can be set up for the porous matrix and fluid independently of each other, there exist a few common boundary conditions which deserve special attention. The following sections refer to the boundary conditions for the system written in Equation 3-11 and Equation 3-12. See derivation in Ref. 7, Ref. 8, and Ref. 9.

The Porous, Free boundary condition is the default for the porous matrix. It means that the displacement of the porous matrix in Equation 3-11 is unconstrained, so it can move freely without experiencing any loads.

The sound soft boundary condition for acoustics creates a boundary condition for Equation 3-12 where the acoustic pressure vanishes, so it sets pf = 0.

For simulating a poroelastic medium bounded by a rigid impervious wall, impose a Fixed Constraint node for the porous matrix displacement in Equation 3-11, u = 0, and a sound-hard boundary condition for the pore pressure in Equation 3-12:

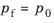
For a given fluid pressure p0 on the boundary, set the pressure in Equation 3-12 to . Since the fluid pressure is set to p0, the normal stress on the porous matrix in Equation 3-11 reduces to

For a rigid porous matrix αB = εp, the load is equivalent to

and for a soft porous matrix αB = 1, there is no load since

For a prescribed displacement u0 at the boundary, set the displacement of the porous matrix in Equation 3-11 as u = u0 and assume a sound-hard (impervious) boundary for the fluid pressure in Equation 3-12:

For a prescribed velocity v0 at the boundary, set the displacement of the porous matrix in Equation 3-11 as

For a prescribed acceleration a0 at the boundary, set the displacement of the porous matrix in Equation 3-11 as

The normal displacement of the porous matrix in Equation 3-11 is constrained, but the porous matrix is free to move in the tangential direction

The impervious (sound hard) boundary condition for the fluid pressure in Equation 3-12 is obtained from

For a prescribed load FA at the boundary, suppose that one side of the septum is fixed to the porous matrix and the other side bears the load.

A septum is a very limp and thin impervious layer with surface density ρsep. Since the septum can be seen as a boundary mass density, this boundary condition is achieved by setting an effective load FS = FA + ρsepω2u on the porous matrix, so the normal stress in Equation 3-11 reduces to