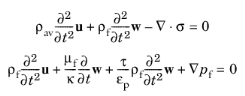In his seminal work, Biot extended the classical theory of linear elasticity to porous media saturated with fluids (Ref. 1, Ref. 2, and Ref. 3).

In Biot’s theory, the bulk moduli and compressibilities are independent of the wave frequency, and can be treated as constant parameters. The porous matrix is described by linear elasticity and damping is introduced by considering the viscosity of the fluid in the pores, which can be frequency dependent. This description is adequate for the propagation of poroelastic waves in soils and rocks where the saturating fluid is a liquid, like oil or water. This formulation is referred to as the Biot model (this is in some sense the classical formulation).

When the considered porous material is saturated by a gas, like air, thermal losses need to be included in order to properly model its behavior. This is the case when modeling sound absorbers, car cabin liners, or foams used in headsets or loudspeakers. The formulation of the equations where both the thermal and viscous losses are included is sometimes referred to as Biot-Allard model. In this case both the viscosity and the fluid compressibility are considered to be frequency dependent and complex valued (Ref. 7, Ref. 8, Ref. 9, Ref. 10, and Ref. 11).

Consider Biot’s expressions for poroelastic waves (Ref. 3, Ref. 4, and Ref. 6)

here, u is the displacement of the porous material, σ is the total stress tensor (fluid and porous material), w is the fluid displacement with respect to the porous matrix, ρf and μf are the fluid’s density and viscosity, τ is the tortuosity, εp is the porosity, pf is the fluid pore pressure, κ is the permeability and ρav the average density. The average density is the total density (porous material plus pore fluid) ρav = ρd + εpρf.

Assuming a time-harmonic dependency for the variables, u(x,t) = u(x)eiωt, w(x,t) = w(x)eiωt, the time derivatives can be removed, so the system in Equation 3-2 becomes

here, the complex density ρc(ω) (Ref. 5) accounts for the tortuosity, porosity, and fluid density, and the viscous drag on the porous matrix

At low frequencies or for small pore sized the flow profile inside the pores can be assumed to be Poiseuille like. In this case the viscosity in Equation 3-4 effectively has a constant value. For increasing frequency the profile changes and a frequency dependent correction factor needs to be taken into account. This is done by selecting the Biot’s high frequency range option from the Viscosity model list. In this case Equation 3-4 is implemented with a frequency-dependent viscosity μc(f) (Ref. 2, Ref. 3, Ref. 5)

here, fr is a reference frequency (SI unit: Hz), which determines the low-frequency range f << fr and the high-frequency range f >> fr.

The reference frequency fr can be interpreted as the limit when viscous forces equal inertial forces in the fluid motion. In a pore with characteristic size a, this happens when the viscous penetration depth is equal to the pore radius.

In the low-frequency limit, viscous effects dominate, while in the high-frequency limit, inertial effects dominate fluid motion in the pores (losses occur in the viscous boundary layer). In Biot’s low frequency range, ω → 0 and Fc = 1.

In order to account for a frequency dependence on the viscous drag, Biot defined the operator Fc(Θ) as

here, T(Θ) is related to the Kelvin functions Ber(Θ) and Bei(Θ)

and J0 and J1 are Bessel functions of the first kind. This expression can be recognized as the loss terms in Zwikker-Kosten like equivalent fluid models (Derivation of the equivalent bulk modulus valid for any fluid in the Zwikker-Kosten theory) or the loss models for cylindrical waveguides in the narrow region acoustics or LRF models (About the Narrow Region Acoustics Models) models.

The formulation in terms of the displacements u and w is not optimal from the numerical viewpoint, since it requires to solve for two displacement fields (Ref. 7, Ref. 8, Ref. 9). The Poroelastic Waves interface solves for the fluid pore pressure variable pf instead of the fluid displacement field w.

The second row in Equation 3-3 is simplified to

so the first row in Equation 3-3 becomes

The total stress tensor σ is then divided into the contributions from the elastic porous (drained) matrix and from the pore fluid

here, the identity tensor I means that the pore pressure pf only contributes to the diagonal of the total stress tensor σ. The parameter αB is the so-called Biot-Willis coefficient. The drained, elastic stress tensor is written as σd = c:ε when ε is the strain tensor of the porous matrix, and the elasticity tensor c contains the drained porous matrix’s elastic properties (see the Linear Elastic Material feature in the Structural Mechanics Module User’s Guide).

Finally, arrange Equation 3-5 in terms of the variables u and p:

The next Biot’s equation comes from taking the divergence of the second row in Equation 3-3, previously divided by −ρc(ω)

Using the expressions for the volumetric strain εvol = ∇·u and fluid displacement (Ref. 3, Ref. 4),

Biot’s modulus M is calculated from the porosity εp, fluid compressibility χf, Biot-Willis coefficient αB and the drained bulk modulus of the porous matrix Kd

so Equation 3-7 simplifies to

and Biot’s wave equations (Equation 3-6 and Equation 3-9) can be written in terms of the variable u and pf as

Further arranging the first row in Equation 3-10 to fit the formulation in the Elastic Waves interface (Equation 3-1) gives

The body load F depends on the angular frequency and the gradient of fluid pressure and the fluid pressure acts as a spherical contribution to the diagonal of Cauchy stress tensor

Arranging the second row in Equation 3-10 to fit the implementation of the Pressure Acoustics, Frequency Domain interface gives (see Theory Background for the Pressure Acoustics Branch)

The monopole domain source Qm (SI unit: 1/s2) and the dipole domain source qd (SI unit: N/m3) depend on the angular frequency ω, the displacement of the porous matrix u, the fluid density and Biot-Willis coefficient αB

When both thermal and viscous losses are included the viscosity in Equation 3-4 and the fluid compressibility in Equation 3-8 are replaced by frequency dependent expressions. The losses due to viscosity are considered by the viscosity expression and the losses due to thermal conduction by the fluid compressibility expression, see Ref. 9.

where the viscous characteristic length Lv has been introduced (it is sometimes referred to as Λ). The frequency dependent complex fluid compressibility is given by

where the thermal characteristic length Lth has been introduced (it is sometimes referred to as Λ’). The two expressions can be recognized in the JCA equivalent fluid model (Johnson-Champoux-Allard (JCA)) available in Pressure Acoustics.