|
|
In the literature, the terms viscoplasticity and creep are often used interchangeably to refer to the class of problems related to rate-dependent plasticity.
|
|
•
|
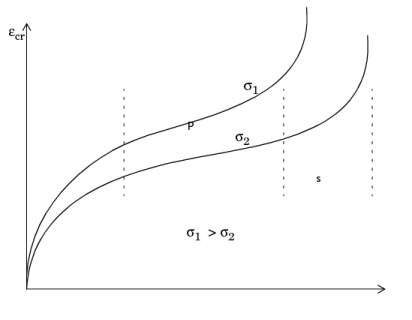
In the initial primary creep regime (also called transient creep) the creep strain rate decreases with time to a minimum steady-state value.
|
|
•
|
In the secondary creep regime the creep strain rate is almost constant. This is also called steady-state creep.
|
|
•
|
In the tertiary creep regime the creep strain increases with time until a failure occurs.
|
In most cases, Fcr1 and
Fcr3 depend on stress, temperature and time, while secondary creep,
Fcr2, depends only on stress level and temperature. Normally, secondary creep is the dominant process. Tertiary creep is seldom important because it only accounts for a small fraction of the total lifetime of a structure.
All creep models are contributing subnodes to the a basic material model like Linear Elastic Material and they can be combined with any other subnodes, such as
Plasticity or
Thermal Expansion to create more advanced models. They can also be combined with each other to model several creep mechanisms acting at the same time.
Here, Qcr is a user-defined creep potential, which is normally written in terms of invariants of the stress tensor.
When (in SI units) the creep potential, Qcr, is given in units of Pa, the rate multiplier
η is given in units of 1/s.
(3-36)
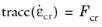
The creep rate, Fcr, usually depends on the first invariant of Cauchy stress
I1(σ) or the pressure
p = −I1/3, in addition to the temperature and other material parameters.
Here, nD is a deviatoric tensor coaxial to the stress tensor.
The creep rate, Fcr, normally depends on the second deviatoric invariant of the stress
J2(σ) or the effective or von Mises (effective) stress
σe, in addition to the temperature and other material parameters.
(3-37)
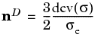
the effective creep strain rate equals the absolute value of the user input
Fcr
where Fcr is a user-defined symmetric tensor field.
The most common model for secondary creep is the Norton equation where the creep strain rate is proportional to a power of the effective stress,
σe:
This is normally true at intermediate to high stress levels and at absolute temperatures of T/
Tm >
0.5, where
Tm is the melting temperature (that is, the temperature in the solid is at least as high as half the melting temperature
Tm). An “Arrhenius type” temperature dependency can also be included. It is defined by
where Q is the activation energy (SI unit: J/mol),
R is the gas constant, and
T is the absolute temperature (SI unit: K).
(3-38)
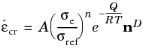
Here, A is the creep rate coefficient (SI unit: 1/s),
n is the stress exponent (dimensionless),
σref a reference stress level (SI unit: Pa), and
nD is a deviatoric tensor coaxial to the stress tensor as defined in
Equation 3-37.
(3-39)
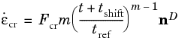
where nD is a deviatoric tensor coaxial to the stress tensor as defined in
Equation 3-37, and
Fcr is expressed as in the Norton model:
(3-40)
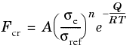
Here, A is the creep rate coefficient (SI unit: 1/s),
n is the stress exponent (dimensionless),
σref is a reference stress level (SI unit: Pa),
tref and
tshift are the reference and shift times (SI unit: s), and
m is the time-hardening exponent (dimensionless).
(3-41)
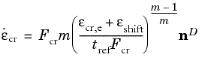
where εcr,e is the effective creep strain, and
εshift is the effective creep strain shift.
Garofalo showed (Ref. 8,
Ref. 9) that the power-law and exponential creep are limiting cases for the general empirical expression
This equation reduces to a power-law (Norton law) for ασe < 0.8 and approaches exponential creep for
ασe > 1.2, where 1
/α is a reference effective stress level.
where Q is the activation energy (SI unit: J/mol),
R is the gas constant, and
T is the absolute temperature (SI unit: K). The complete creep rate equation as used in COMSOL Multiphysics then reads
where, A is the creep rate (SI unit: 1/s),
n is the stress exponent (dimensionless), and
σref a reference effective stress level (SI unit: Pa).
nD is a deviatoric tensor coaxial to the stress tensor as defined in
Equation 3-37.
At low stress levels and high temperatures, Navarro and Herring (Ref. 6,
Ref. 7) independently derived an expression for the creep rate as a function of atomic diffusion
Here, d is the grain diameter,
Dv is the volume diffusivity through the grain interior,
b is Burgers vector,
kB is the Boltzmann’s constant, and
T is the absolute temperature.
nD is a deviatoric tensor coaxial to the stress tensor as defined in
Equation 3-37.
Coble creep (Ref. 6,
Ref. 7) is closely related to Navarro-Herring creep but takes into account the ionic diffusivity along grain boundaries
Dgb
At intermediate to high stress levels and temperatures T/Tm > 0.5, the creep mechanism is assumed to be diffusion-controlled movements of dislocations in the crystal lattices (
Ref. 7)
where and nD is a deviatoric tensor coaxial to the stress tensor as defined in
Equation 3-37. Generally, the stress exponent
n takes values between 3 and 5.
Here, T is the temperature,
d is the grain size,
b is the Burgers vector,
D is the self diffusion coefficient,
G is the shear modulus, and
e−Q/RT is an “Arrhenius” type of temperature dependency.
For high temperatures, Mukherjee-Bird-Dorn equation describes Weertman creep when setting p = 0. Setting
n = 0 and
p = 2 describes Nabarro-Herring, and setting
n = 0 and
p = 3 describes Coble creep. Harper-Dorn creep is obtained by setting
n = 1 and
p = 0.
The Anand viscoplasticity (Ref. 9) is a deviatoric creep model suitable for large, isotropic, viscoplastic deformations in combination with small elastic deformations.
where nD is a deviatoric tensor coaxial to the stress tensor as defined in
Equation 3-37, and the creep rate is calculated from
Here, A is the creep rate coefficient (SI unit: s
−1),
Q is the activation energy (SI unit: J/mol),
m is the stress sensitivity,
ξ is the multiplier of stress,
R is the gas constant, and
T is the absolute temperature (SI unit: K).
The internal variable, sa, is called
deformation resistance (SI unit: Pa) and is calculated from the rate equation
with the initial condition sa(0) = sinit. Here,
h0 is the
hardening constant (SI unit: Pa), and
a is the
hardening sensitivity.
The variable sa* is the saturation value of the deformation resistance
sa, which is calculated from the expression
where s0 is the
deformation resistance saturation coefficient (SI unit: Pa), and
n is the
deformation resistance sensitivity.
Here, A is the viscoplastic rate coefficient (SI unit: 1/s),
n is the stress exponent (dimensionless),
σref a reference stress level (SI unit: Pa), and
nD is a deviatoric tensor coaxial to the stress tensor. The Macaulay brackets are applied on the yield function, which is defined as done for plasticity
The effective stress φ(σ) is either the von Mises, Tresca, or Hill stress; or a user-defined expression, and
σys is the yield stress (which may include a linear or nonlinear
Isotropic Hardening model). The stress tensor used in the effective stress
φ(σ) is shifted by what is usually called the
back stress,
σback when
Kinematic Hardening is included.
The deviatoric tensor nD is computed from the plastic potential
Qp
When von Misses effective stress is used, the associated flow rule reads Qp = Fy, and the deviatoric tensor
nD is defined as done for deviatoric creep
(3-42)
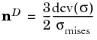
|
|
When the Calculate dissipated energy check box is selected, the dissipation rate density due to creep is available under the variable solid.Wcdr and the dissipation rate density due to viscoplasticity is available under the variable solid.Wvpdr. The dissipated energy density due to creep is available under the variable solid.Wc and due to viscoplasticity under the variable solid.Wvp. Here solid denotes the name of the physics interface node.
|
The equation forms described in for the different creep models above differ from the forms most commonly found in the literature. The difference lies in the introduction of normalizing reference values such as the reference stress σref and reference time t
ref. These values are in a sense superfluous, and can in principle be chosen arbitrarily. The choice of reference values will however affect the numerical values to be entered for the material data. This system has two advantages
The coefficient AN has a physical dimension which depends on the value of
n and the unit have an implicit dependence on the stress and time units. Converting the data to the form used in COMSOL Multiphysics (
Equation 3-38) requires the introduction of the reference stress
σref. It is here convenient to use the implicit stress unit for which
AN is given as reference stress. The creep rate coefficient
A will then have the same numerical value as
AN, and you do not need to do any conversions.
The physical dimension of A is however (
time)-1, whereas the physical dimension of AN is (stress)-n(time)-1.
Another popular way of representing creep data is to supply the stress giving a certain creep rate. As an example, σc7 is the stress at which the creep strain rate is
10-7/h. Data on this form is also easy to enter: You set the reference stress to the value of
σc7, and enter the creep rate coefficient as
1e-7[1/h].
|
•
|
σc7 = 70 MPa, and stress exponent n = 4.5.
|
|
•
|
AN = 4.98 ·10-16 with respect to units MPa and hours, and stress exponent n = 4.5.
|
In this case, the coefficient ANB has implicit dimension and units which depend on the values of
n and
m, and on the stress and time units.
Converting the data to the form used in COMSOL Multiphysics (Equation 3-39 and
Equation 3-40) requires the introduction of an both an arbitrary reference stress
σref and an arbitrary reference time t
ref. If you use the implicit units for which
ANB is given as the reference values, then the constant
A will have the same numerical value as
ANB.
