Generator in 2D

This example shows how the circular motion of a rotor with permanent magnets generates an induced EMF in a stator winding. The generated voltage is calculated as a function of time during the rotation. The model also shows the influence on the voltage from material parameters, rotation velocity, and number of turns in the winding.

The center of the rotor consists of annealed medium carbon steel, which is a material with a high relative permeability. The center is surrounded with several blocks of a permanent magnet made of samarium and cobalt, creating a strong magnetic field. The stator is made of the same permeable material as the center of the rotor, confining the field in closed loops through the winding. The winding is wound around the stator poles. Figure 1 shows the generator with part of the stator sliced in order to show the winding and the rotor.

Figure 1: Drawing of a generator showing how the rotor, stator, and stator winding are constructed. The winding is also connected between the loops, interacting to give the highest possible voltage.

Modeling in COMSOL Multiphysics

The COMSOL Multiphysics model of the generator is a time-dependent 2D problem on a cross section through the generator. This is a true time-dependent model where the motion of the magnetic sources in the rotor is accounted for in the boundary condition between the stator and rotor geometries. Thus, there is no Lorentz term in the equation, resulting in the PDE

where the magnetic vector potential only has a z component.

Rotation is modeled using a ready-made physics interface for rotating machinery. The center part of the geometry, containing the rotor and part of the air-gap, rotates relative to the coordinate system of the stator. The rotor and the stator are imported as two separate geometry objects, so it is possible to use an assembly (see Finalizing the Geometry in the COMSOL Multiphysics Reference Manual for details). This has several advantages: the coupling between the rotor and the stator is done automatically, the parts are meshed independently, and it allows for a discontinuity in the vector potential at the interface between the two geometry objects (called slits). The rotor problem is solved in a rotating coordinate system where the rotor is fixed (the rotor frame), whereas the stator problem is solved in a coordinate system that is fixed with respect to the stator (the stator frame). An identity pair connecting the rotating rotor frame with the fixed stator frame is created between the rotor and the stator. The identity pair enforces continuity for the vector potential in the global fixed coordinate system (the stator frame).

The stator and center of the rotor are made of annealed medium-carbon steel (soft iron), which is implemented in COMSOL Multiphysics as an interpolation function of the B-H curve of the material; see Figure 2. The function can be used in the domain settings. Usually B-H curves are specified as |B| versus |H|, but the rotating machinery, magnetic interface must have |H| versus |B|. It is therefore important that the H-data is entered as f(x)-data of the interpolation function and the B-data entered as x-data. This relationship for |H| is predefined for the material Soft Iron (without losses) in the materials library that is shipped with the AC/DC Module.

Figure 2: The norm of the magnetic flux, |B|, versus the norm of the magnetic field, |H|, for the rotor and stator materials. The inverse of this curve is used in the calculation.

The generated voltage is computed as the line integral of the electric field, E, along the winding. Because the winding sections are not connected in the 2D geometry, a proper line integral cannot be carried out. A simple approximation is to neglect the voltage contributions from the ends of the rotor, where the winding sections connect. The voltage is then obtained by taking the average z component of the E field for each winding cross-section, multiplying it by the axial length of the rotor, and taking the sum over all winding cross sections.

where L is the length of the generator in the third dimension, NN is the number of turns in the winding, and A is the total area of the winding cross-section.

Results and Discussion

The generated voltage in the rotor winding is a sinusoidal signal. At a rotation speed of 60 rpm the voltage has an amplitude slightly above 4 V for a single turn winding; see Figure 3.

Figure 3: The generated voltage over one quarter of a revolution. This simulation used a single-turn winding.

The norm of the magnetic flux, |B|, and the field lines of the B field are shown below in Figure 4 at time 0.20 s.

Figure 4: The norm and the field lines of the magnetic flux after 0.2 s of rotation. Note the brighter regions, which indicate the position of the permanent magnets in the rotor.

ACDC_Module/Motors_and_Actuators/generator_2d

Modeling Instructions

From the menu, choose .

New

In the window, click .

Model Wizard

In the window, click .

In the tree, select .

Click .

In the tree, select .

Click .

Global Definitions

Parameters

On the toolbar, click .

In the window for , locate the section.

In the table, enter the following settings:


Name	Expression	Value	Description
L	0.4[m]	0.4 m	Length of generator
rpm	60[1/min]	1 1/s	Rotational speed of rotor
A	pi*(3[cm]/2)^2	7.069E-4 m²	Area of single circular conductor coil

Geometry 1

Import 1 (imp1)

Import the geometry of the generator cross section from an external CAD file.

On the toolbar, click .

In the window for , locate the section.

Click .

Browse to the model’s Application Libraries folder and double-click the file generator_2d.mphbin.

Click .

Form Union (fin)

The geometry you imported is composed by two objects, an inner part (corresponding to the rotor) and an outer part (the stator). Create an assembly from these objects.

In the window, under click .

In the window for , locate the section.

From the list, choose .

On the toolbar, click .

In this way, an identity pair connecting the shared boundaries has been automatically created.

Definitions

Cylindrical System 2 (sys2)

On the toolbar, click and choose .

The cylindrical coordinate system you just added will be used to define the field of the permanent magnets.

Add Material

On the toolbar, click to open the window.

Go to the window.

In the tree, select .

Click in the window toolbar.

Add Material

Go to the window.

In the tree, select .

Click in the window toolbar.

Materials

Soft Iron (without losses) (mat2)

In the window, under click .

Select Domains 2 and 28 only.

On the toolbar, click to close the window.

Rotating Machinery, Magnetic (rmm)

In the window, under click .

In the window for , locate the section.

In the d text field, type L.

Apply a Prescribed Rotational Velocity feature to the rotor, and specify its rotational velocity using the parameter rpm.

Prescribed Rotational Velocity 1

Right-click and choose .

Select Domains 19–28 only.

In the window for , locate the section.

In the rps text field, type rpm.

The permanent magnets on the rotor have a radial field. Use the cylindrical coordinate system specified earlier to define it.

Ampère’s Law 2

In the window, right-click and choose the domain setting .

Select Domains 20, 23, 24, and 27 only.

In the window for , locate the section.

From the list, choose .

Locate the section. From the list, choose .

Specify the Br vector as


0.84[T]	r
0	phi
0	a

Right-click and choose .

In the dialog box, type Permanent Magnets Outward in the text field.

Click .

The other four magnets are reversed.

Ampère’s Law 3

In the window, right-click and choose the domain setting .

Select Domains 21, 22, 25, and 26 only.

In the window for , locate the section.

From the list, choose .

Locate the section. From the list, choose .

Specify the Br vector as


-0.84[T]	r
0	phi
0	a

Right-click and choose .

In the dialog box, type Permanent Magnets Inward in the text field.

Click .

Ampère’s Law 4

In the window, right-click and choose the domain setting .

In the window for , locate the section.

From the list, choose .

Select Domains 2 and 28 only.

Right-click and choose .

In the dialog box, type Iron in the text field.

Click .

Coil 1

In the window, right-click and choose the domain setting .

Select Domains 3–18 only.

In the window for , locate the section.

From the list, choose .

In the Icoil text field, type 0[A].

Locate the section. In the N text field, type 1.

In the acoil text field, type A.

Locate the section. Select the check box.

Reversed Current Direction 1

Right-click and choose .

Click the button on the toolbar.

Select Domains 3, 4, 9–12, 17, and 18 only.

The problem will be solved separately in the fixed frame of the stator and the rotating frame of the rotor. Apply a Continuity feature on the shared boundaries (that are connected by ).

Continuity 1

In the window, right-click and choose .

In the window for , locate the section.

In the list, select .

Mesh 1

Size

In the window, under right-click and choose .

In the window for , locate the section.

From the list, choose .

Click the button.

Locate the section. In the text field, type 2.

Click .

Study 1

Step 2: Time Dependent

On the toolbar, click and choose .

In the window for , locate the section.

In the text field, type range(0,0.01,0.25).

Some adjustments to the solver settings are required in order to obtain a more stable solution.

Solution 1 (sol1)

On the toolbar, click .

In the window, expand the node, then click .

In the window for , click to expand the section.

Locate the section. From the list, choose .

Find the subsection. From the list, choose .

In the window, expand the node, then click .

In the window for , click to expand the section.

Click to expand the section. Locate the section. From the list, choose .

In the text field, type 1e-3.

On the toolbar, click .

Results

Magnetic Flux Density (rmm)

In the window, under click .

In the window for , locate the section.

From the list, choose .

Contour 1

In the window, expand the node, then click .

In the window for , locate the section.

In the text field, type 12.

On the toolbar, click .

The plot will show the rotor position at t = 0.2 s, the magnetic flux density norm and magnetic flux lines. Next, plot the induced EMF in a quarter of the cycle.

1D Plot Group 2

On the toolbar, click and choose .

In the window for , click to expand the section.

From the list, choose .

In the text area, type Induced voltage.

Locate the section. Select the check box.

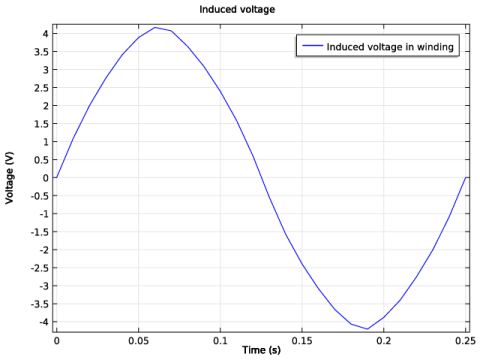
In the associated text field, type Time (s).

Select the check box.

In the associated text field, type Voltage (V).

Global 1

Right-click and choose .

In the window for , click in the upper-right corner of the section. From the menu, choose .

On the toolbar, click .

The plot shows an induced EMF with an amplitude of about 4.2 V