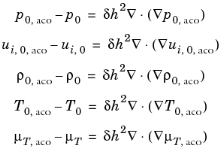When the aeroacoustic and the CFD model are not solved on the same computational mesh, careful mapping of the CFD solution from the CFD mesh onto the acoustics mesh should be done. This step is crucial in order not to introduce non-physical numerical noise into the acoustic solution (Ref. 20). If the solution is not properly mapped terms containing gradients of the background mean flow variables become very noisy and are typically the source of the error. If the acoustic problem is solved on the same mesh as the CFD then the mapping problem is less of an issue.

If two different mesh and/or different shape function orders are used in the acoustic and the CFD models a mapping study needs to be used. This is a study that solves an additional set of equations which maps and smooths the background flow CFD variables onto the acoustics mesh. The mapping equations can be set up using the Weak Form PDE interface from the Mathematics branch. In the most general case the mean background flow pressure p0, velocity field u0, density ρ0, temperature T0, and turbulent viscosity μT variables should be mapped onto corresponding variables on the acoustics mesh, for example, p0,aco, u0,aco, ρ0,aco, T0.aco, and μT,aco. These new variables should then be used as the model inputs in the aeroacoustics model.

where the term on the right hand side adds smoothing using isotropic diffusion. The amount of diffusion is controlled by the parameter δ (a constant that can be tuned with a typical value of 0.01) and the mesh size squared h2. The term corresponds to so-called source term stabilization as known from CFD.

In the Weak Form PDE interface define as many dependent variables as necessary and give them the same shape order as the order used for the acoustics (typically all linear). Assume that the source CFD variable for the x-velocity component is u and the new destination variable is U0, then the above mapping is achieved with the following Weak Expression, entered in the user interface:

For the pressure map the total pressure spf.pA to P0 using:

Notice the use of the withsol() operator which is an extrusion-like coupling operator that can refer directly to a solution object and parameter value. In this example it is used to fetch data from the CFD mesh, in the solution generated by solver sol1 and for the parameter value Ma = 0.1. The setval() statement is optional. It is important to use such an operator such that the CFD solution is mapped and interpolated correctly to the integration (Gauss) points on the acoustics mesh.

In some cases it can be necessary to extend the mapping equation with boundary conditions for the mapped variables. This should be done at symmetry planes for the mapped velocity field. This is also the cases when flow details near walls are important, for example, resolving the acoustic boundary layer. In this case add a no-slip condition on u0,aco. In general constraining the value of the mapped variables to the value in the CFD model values at boundaries can be necessary.