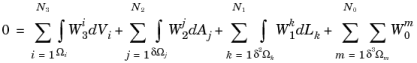Note that all contributions are summed into the same integral equation without any particular order. Therefore, whether you write two equations in separate contributions or sum them into one single contribution normally does not matter. There is, however, a small caveat: the index on dVi,
dAj, and
dLk indicate that each contribution may be integrated in a different way. The integration can be performed with respect to either material or spatial coordinates and, in addition, using different numerical quadrature orders. But while working inside a single PDE interface, all contributions are integrated in the same way.
on the boundary level. Gammax and
Gammay are variables representing the components of
Γ, and
f and
G are variables representing
f and
G, respectively.
When a nonlinear expression — for example, a Green-Lagrange strain — is inserted into the test operator, the operator acts as a linear differential operator. This means that the argument expression is effectively first differentiated with respect to each dependent variable it contains, and the results are then multiplied by the test function of the corresponding variable. Therefore, the heat equation may alternately be implemented as
q*test(u)-0.5*k*test(ux^2+uy^2). Using the chain rule on the second term with the
test operator as the differential operator returns the standard weak form of the equation given above.
In another example, test(F(u,
∇u)), the
test operator is equivalent to: