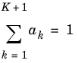Weighted Sum of Gray Gases Model (WSGG)
As for other polychromatic radiation models, the weighted-sum-of-gray-gases method aims to account for wavelength dependence of emission through material properties (Ref. 23); see the section Wavelength Dependence of Surface Properties.
In the scope of this method, instead of defining constant properties per band, the real nongray gas is replaced by a mix of virtual gray gases in certain proportions. Each of them has a different absorption coefficient such that, once all summed, they are representative of the real gas behavior over the whole wavelength spectrum.
For a mix of K+1 virtual gray gases, weight factors a are defined to account for the proportion of each gray gas in the mix, they verify the following property:
The first gas, with index 1, is always a transparent gas that accounts for the spectral windows where absorption is negligible. The absorption coefficient of this gas, κ1, is therefore 0. With this approach, the absorption coefficients are constant for each gray gas, but the weight factors may depend on temperature.
In the Discrete Ordinates Method (DOM), the Radiative Transfer Equation is solved for each gray gas:
Note that σs has no index k since the same scattering coefficient is used for all gray gases.
If the P1 Approximation Theory is used instead, the incident radiation Gk for the gray gas k is solution of the following equation,
(4-137),
where
•
DP1,k is the P1 diffusion coefficient, defined as
•
a1 is the linear Legendre coefficient of the scattering phase function, not to be confused with the weight factor of the first gray gas, which shares the same notation.
•
Qr,k is the radiative heat source:
(4-138).