Deriving the Directional Dependence of Surface Properties for Refractive Interface
A refractive interface may reflect or transmit any incoming radiation depending on the angle of incidence, and the refractive indices of the surrounding media. The reflectance and transmittance can be derived with the help of Fresnel’s relations. The Figure 4-16 shows how an incoming ray is reflected and refracted through a refractive interface.
Figure 4-16: Ray path through a refractive interface.
For the following derivation, it is supposed that the imaginary part of the refractive index is negligible.
The interface is optically flat (specular). The reflection and transmission at the interface is calculated starting with Snell’s law:
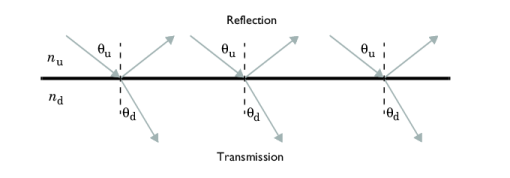
Here, nu and nd are the refractive indices of the adjacent domains. The angle of incidence θu and the angle of transmission θd are measured with respect to the surface normal so they correspond to the polar angles with the refractive surface.
The Fresnel coefficients give the reflection coefficients of each s- and p-polarization:
The reflected power of each polarization at the interface is given by
Thermal radiation is randomly polarized because it is a result of multiple incoherent combinations between variously polarized wave trains. Therefore, one can take the average of the s- and p-polarization to compute reflection and transmission of the interface:
The reflection, and therefore the transmission, is identical on the incident and transmitted sides for each interface, for example, Ru → d = Rd → u.
The directional specular reflectivity of the interface is thus
Since the directional absorptivity function, and thus the directional emissivity function, of the interface is zero, it follows that , and we obtain the transmissivity through the interface:
Once the directional function of surface properties are calculated, there remains an issue to handle. When nu > nd, the angle of transmission θd is greater than the angle of incidence θu. This leads to the appearance of a critical angle θc above which θd cannot be calculated because the arcsine is only defined in the interval [−1, 1]. The critical angle is
Which is the value of θu that leads to θd equal to π/2. Above this critical angle, all the incident radiation is reflected and nothing is transmitted. When nu > nd, the arcsine is well defined for the whole range of θu.