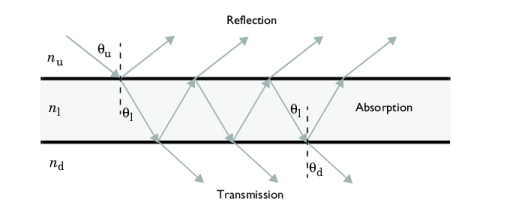
Where nu and
nd are the refractive indices of the adjacent domains, and
nl is the refractive index of the layer. The angle of incidence
θu is measured with respect to the surface normal so it corresponds to the polar angle with the semitransparent surface. The angle of the ray within the material is noted
θl, and the angle of the ray in the downside domain is noted
θd.