The Free and Porous Media Flow, Darcy interface uses the Navier–Stokes equations to describe the flow in the free-flow region, implemented by the coupled Laminar Flow interface, and Darcy’s law, implemented by the coupled Darcy’s Law interface, to describe the flow in the porous region.

In the free-flow region, the velocity u and pressure p are solved for, whereas in the porous region only the pressure p is solved for, and the velocity is calculated from the pressure by Darcy’s law.

Here ρns and uns are the density and velocity on the free-flow side of the interface, ρd and ud the density and velocity on the porous side, and n is a vector normal to the interface. In addition the coupling enforces the balance of the normal forces by:

where pns and pd are the pressure on the free-flow side and porous side of the interface, respectively, and K is the viscous stress tensor (defined only on the free-flow side). The Include pressure jump across free-porous boundary option allows to specify an additional pressure jump pj, in order to model, for example, a resistive layer or other pressure losses at the free-porous interface, such that the balance of the normal forces reads:

For the coupling condition for the tangential velocity component, there are several options. One of the most widely used conditions is the Beavers–Joseph interface condition (Ref. 1):

where aBJ is the Beavers and Joseph parameter, κ is the permeability tensor of the porous medium (defined on the porous side of the interface), μns is the fluid’s dynamic viscosity on the free-flow side of the interface, and n is the number of space dimensions.

When the velocity in the porous domain is much smaller than the velocity in the free flow, one can use a modification of the Beavers–Joseph condition which is given by the Beavers–Joseph–Saffman interface condition (Ref. 2):

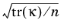
For cases when the permeability tensor is not isotropic, the Use projected permeability option allows to take into account only the permeability in the direction of the tangential velocity component. This is accomplished by replacing the term on the rights hand side of Equation 7-39 and Equation 7-40 by

with t a unit vector tangent to the interface for 2D and 2D-axisymmetric cases, and for 3D cases by

with v given by

If one considers the limit of the Beavers–Joseph condition for large values of the Beavers and Joseph parameter aBJ, one obtains the Continuous tangential velocity condition:

The same limit for the Beavers–Joseph–Saffman condition results in the No slip condition:

The Viscous slip condition allows for a more general coupling condition. This interface condition is given by

Here Ls is a slip length, and ub a user-defined interfacial velocity.