Impedance
Use the Impedance node in frequency domain analysis to define the specific (input) impedance of an external domain, as the ratio of pressure to normal velocity Zn = p/(n · v), at the boundary. The impedance can, for example, represent an acoustic liner in a doc acoustics problem such as a turbofan engine. Two options exist for the impedance condition:
•
The Ingard–Myers condition, that assumes that the background mean flow boundary layer (hydrodynamic boundary layer) is infinitely thin (see Ref. 1 and Ref. 2),
•
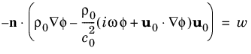
and the Brambley condition, which represents an extension to the Ingar-Myers formulation. For the Brambley option refraction effects of the background mean flow boundary layer are included, assuming a finite linear profile thickness δ, see Ref. 28 and Ref. 29. In this way, important flow effects can be included, while still using a compressible potential flow as the background mean flow, see Ref. 30.
In linearized potential flow, the impedance boundary condition is in general given as
where, for the Ingard–Myers formulation, w is defined as
and, for the Brambley formulation, w is defined as
Impedance
Select the Impedance model as either Ingard–Myers (the default) or Brambley (finite boundary layer).
•
For both options enter the Specific impedance Zn (SI unit: Pa·s/m).
•
For the Brambley (finite boundary layer) option also enter the Turbulent boundary layer thickness (background mean flow) δ (SI unit: m).
For a tutorial that compares the Brambley (finite boundary layer) with, the detailed and more computationally expensive, linearized Navier–Stokes formulation, see the Generic Nacelle with an Acoustic Liner tutorial. Application Library path:
Acoustics_Module/Aeroacoustics_and_Noise/generic_nacelle_liner