The Phase Field in Solids interface solves an Allen–Cahn-type of a reaction-diffusion equation. This equation is commonly used for regularized modeling of the evolution of sharp interfaces such as cracks, damage, and grain boundaries in solids. The equation is based on the phase-field theory of fracture presented in Ref. 166. The central idea relies on approximating the set Γ that represents sharp interfaces by a regularized crack functional

Here, the so-called crack surface density function γ(ϕ, ∇ϕ) is a function of the phase field ϕ and its gradient ∇ϕ, which is defined in the whole domain Ω instead of only on the crack surfaces. The crack surface density function γ also depends on the internal length scale lint that controls the regularization, which means that Γl → Γ for lint → 0.

The evolution of the functional is written (Ref. 167)

where Sl is a driving source term, Rl is a viscous resistance term, and the inequality indicates the irreversibility of processes like damage and fracture. For a general crack surface density function with source and viscous resistance terms of the form

the local form of Equation 3-271 can be derived as

Herein, τ is a viscous regularization time constant and f is a local source term. In the derivation, homogeneous Neumann conditions are assumed on the external boundaries of the domain, that is,

where N is the normal to the undeformed surface.

A common form for the crack surface density function is isotropic and quadratic in the phase field and its gradient (for example, Refs. 166–168)

By inserting Equation 3-275 into Equation 3-273, the strong form of the phase field equation reads

The weak form of Equation 3-276 is the default equation solved in the Phase Field in Solids interface.

Alternative phase field models of fracture have considered a crack surface density function that deviate from the local quadratic term ϕ2 and include anisotropy in the form of a structure tensor D in the nonlocal term (see Ref. 168 for a review). In the Phase Field in Solids interface, such a generalization of Equation 3-276 that also includes an extension to multiple phase fields ϕk is written as

Here, the potential function has been introduced. Equation 3-276 is recovered for the quadratic potential

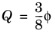
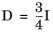
and the structure tensor Dk = I, which corresponds to the so-called AT2 phase-field model. Similarly, the AT1 phase-field model is obtained by setting and . Note that, in absence of a source term f, the quadratic form of the AT2 model has the advantage of admitting the trivial solution ϕ = 0 as well as guaranteeing that the solution is bounded, ϕ ∈ [0, 1] (Ref. 166). If required, bounds on the phase field variable can be added in terms of weak inequality constraints; see Bounds in The Phase Field in Solids Interface.