Wrinkling
Due to the zero bending stiffness assumption, the numerical treatment of thin structures is much simpler with the membrane theory as compared to shell theory. However, this assumption is disadvantageous in some cases such as wrinkling, which happens when the membrane is subjected to negative principal stresses.
A thin shell will wrinkle when the compressive stress reaches a critical level defined by its bending stiffness, which is a local buckling phenomenon. When such thin structures are modeled within the membrane theory, wrinkles appear at the onset of the compressive stresses as the bending stiffness is assumed to be zero. Due to zero bending stiffness such states can be represented by continuously distributed infinitesimal wrinkles.
When using the traditional membrane theory, which does not incorporates a wrinkling model, negative principal stresses result in an equilibrium instability. In order to overcome this instability, the wrinkling model within the framework of the tension field theory can remove compressive stresses from wrinkled regions resulting in a correct stress distribution, Ref. 163–165.
The modified membrane theory, which incorporates a wrinkling model to the traditional membrane theory, disregards the out-of-plane deformation in wrinkling; so wrinkles including details like their amplitude and wavelength are determined on the mean surface of the membrane (Ref. 163–165).
There are two approaches to embed the tension field theory into the framework of classical membrane theory, but essentially both approaches are equivalent (Ref. 165). One approach is to replace the strain energy density with a relaxed variant of it, while the other approach is to modify the deformation gradient (Ref. 163). While the first approach can only be used for isotropic membranes, the second approach is more general (Ref. 163), and it is the method implemented in COMSOL Multiphysics.
The undeformed configuration of the membrane is described by the material coordinates X, Y, and Z. The uniaxial stress occurs in the X direction; Y is the wrinkling direction and Z is the normal to the membrane plane (Figure 3-59). The deformed configuration is represented by the x, y, and z coordinates. After deformation, the membrane can be in one of three possible states:
•
A taut state, which is achieved when both in-plane principal stresses are positive, and there is no need to modify the deformation tensor.
•
A wrinkled state, which happens when one of the principal stresses is negative. A modification to the deformation gradient tensor is necessary.
•
A slack state, reached when both in-plane principal stresses are negative. In this case, the stress tensor is set to be zero.
As shown in Figure 3-59 there are three different kinematic descriptions (Ref. 163):
•
The tensor F* maps the reference configuration to the true wrinkled configuration. This mapping is not suitable to describe the strain field in wrinkled membranes.
•
The tensor F maps the reference configuration to the mean configuration, where the current area is smaller than the actual wrinkled area. Hence, this mapping is also not suitable to describe the strain field in wrinkled membranes.
•
The tensor maps the reference configuration to a fictitious lengthened configuration, where the current area is equal to the actual wrinkled area. This mapping is suitable to describe the strain field in wrinkled membranes.
Figure 3-59: Kinematics of wrinkling.
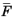
When n1 is the direction of uniaxial extension, and assuming that wrinkling occurs in the n2 direction, the modified deformation tensor is written as
(3-250)
Here, ⊗ is the outer product of two vectors, (a⊗b)ij = aibj, and β is the wrinkling parameter, so β = 0 represents a taut condition. According to the orthogonality condition in tension field theory, these two vectors satisfy
(3-251)
where σ is the Cauchy stress tensor written in terms of the second Piola–Kirchhoff stress tensor
Assuming that the mean configuration F is known, the only unknowns in Equation 3-250 and Equation 3-251 are β and n2.
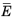
Since the material properties and membrane theory itself are given in the reference configuration, Equation 3-250 and Equation 3-251 are transformed to the reference configuration (Ref. 164). The fictive Green–Lagrange strain tensor is then written with the help of a vector in the reference configuration which corresponds to the wrinkling direction n2, so g = n2⋅F,
This can be written as
where βm and N2 are the wrinkling parameter and wrinkling direction in the reference configuration. The two unknowns β and n2 in the deformed configuration are replaced by the two unknowns βm and N2 in the reference configuration.
The membrane surface is spanned by a coordinate system having two in-plane orthogonal unit vectors e1 and e2. Thus, N1 and N2 can be written with the help of the wrinkling angle αm
So the scalar wrinkling angle αm is sufficient to define the wrinkling vector N2. The two nonlinear equations in Equation 3-251 are then solved for the two unknowns αm and βm with the Newton-Raphson method. Once the parameters αm and βm are determined, the deformation gradient and the second Piola–Kirchhoff stress tensor are modified to get the correct stress distribution and to define the wrinkled regions.