Symmetry Planes
The model geometry may contain mirror and sector symmetries, as well as plane, rigid end caps. In such cases, the model geometry does not form a closed surface and further information is required to compute the total volume. The figure below shows a few such examples in 2D. The first two examples show circular cavities, where only part of the volumes are modeled due to mirror symmetries. The third example shows part of a toroidal structure, where the model is reduced due to sector symmetry. The last case shows a pressure vessel mounted on a rigid foundation, which is not explicitly modeled.
Figure 3-50: Example positions of the reference point and volume factor when modeling cavities bounded by symmetry planes, or rigid end caps/foundation planes.
To compute the volume in the cases shown above, it is necessary to select a reference point, Xref. The reason is that the flux vector used to compute the volume must not penetrate any symmetry plane or plane end cap. The following rules apply when selecting the reference point, Xref:
•
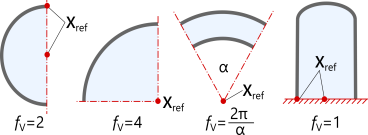
For half symmetry (one plane), Xref may be an arbitrary point on the symmetry plane. In case the model is 2D axisymmetric, Xref is the intersection of the symmetry plane with the axisymmetry axis (that is, Xref is located at R = 0).
•
For quarter symmetry (two orthogonal planes), Xref may be an arbitrary point on the intersection of the symmetry planes. In 2D this is a well-defined point.
•
For eighth symmetry (three orthogonal planes), Xref must be the intersection point of the symmetry planes. This case is only applicable in 3D.
•
For rotational symmetry (sector symmetry), Xref must be an arbitrary point on the rotational axis. In 2D this is a well-defined point.
•
For a plane end cap, Xref may be an arbitrary point on the end cap plane. The cavity must only have a single end cap plane.
The volume factor, fV, shown in the figure above, is defined as the ratio between the true volume and the actual volume included in the model. For example, for a simple mirror symmetry, fV is equal to two, meaning that the true volume is twice as large as the volume represented by the model geometry.