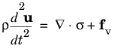Electromechanics
The Electromechanics, Solid Interface theory is described in this section:
•
Overview of Forces in Continuum Mechanics
•
The Electromagnetic Stress Tensor
•
Large Deformations
•
About Different Stress Forms
•
References for the Electromechanics Interface
Overview of Forces in Continuum Mechanics
The deformation of elastic materials subject to external loads is described by the momentum balance equation:
where ρ is the density, u denotes the structural displacement vector, σ is the stress tensor, and fv is an external volume force (such as gravity).
In the stationary case, there is no acceleration, and the equation representing the force balance is
The stress tensor must be continuous across a stationary boundary between two materials. This corresponds to the equation
(3-156)
where σ1 and σ2 represent the stress tensor in Materials 1 and 2, respectively, and n1 is the normal vector pointing out from the domain containing Material 1.
The Electromagnetic Stress Tensor
Within a vacuum or other medium, forces between charged bodies can be computed on the assumption that a fictitious state of stress exists within the field. Historically the consistency of this approach led 19th-century physicists to postulate the existence of the ether, a ubiquitous medium through which electromagnetic forces propagate. While these ideas have been superseded by the development of special relativity, the use of an electromagnetic stress tensor (also known as the Maxwell stress tensor) remains an accurate and convenient technique to compute electromagnetic forces.
Maxwell stresses exists in all dielectric materials, including air and even free space. However, the force magnitude is rather small, and it usually can cause significant deformations only at small dimension.
The electromagnetic stress tensor in a vacuum (in the absence of magnetic fields) is given by (Ref. 145):
(3-157)
Where E is the electric field, I is the identity tensor, ε0 is the permittivity of free space, and
Within an isotropic linear dielectric under small deformations, the electric displacement vector is related to the electric field as (Ref. 146):
where the electric susceptibility χ can be a function of the mechanical strain in the material
where the small strain tensor is given by
The corresponding electromagnetic tress tensor takes the following form:
(3-158)
where the relative permittivity of the material with the absence of deformation is introduced as εr = 1 + χ0. It can be written equivalently as
where the two terms represent, respectively, the contributions from: the underlying free space and the material polarization.
The Electromechanics coupling feature applies the material and underlying free space contributions to the stress as a body load. In weak form: −σEM : test(T).
Large Deformations
For finite deformations, the expressions for the electromagnetic stress and material polarization can be derived using the following thermodynamic potential called electric enthalpy:
where the subscript m indicates that the vector components must be taken on the material frame, and the right Cauchy–Green deformation tensor is
with F = ∇u + I and J = det(F). The mechanical energy function Ws(C) depends on the solid model used.
The total second Piola–Kirchhoff stress tensor is given by
and the electric displacement can be calculated as
The electromagnetic stress tensor can be used to compute the forces acting on a dielectric body. From Equation 3-156 the balance of forces at the surface of a dielectric body (material 1) in vacuum or air (material 2) implies:
where the total stress tensors in media 1 and 2 are, respectively:
where σm is a mechanical component of the total stress and the ambient pressure p2 in to surrounding air or other medium (if present). Using Equation 3-167:
where the electric field E is computed in material 2.
The Electromechanics coupling feature applies the above defined traction as a boundary load on the boundaries which are external for the coupling feature selection but internal for the corresponding Electrostatics interface.
COMSOL Multiphysics does not explicitly include the ambient pressure definition on the Electromechanical Forces coupling feature. However, it is possible to add an additional surface force to the corresponding Solid Mechanics interface if the pressure is known or computed by another physics interface.
About Different Stress Forms
There exists a long-lasting controversy in scientific literature about the definition of electromagnetic forces acting on solids. An extensive review can be found in Ref. 137. Many classic textbooks (for example, Ref. 145 and Ref. 146) operate with the so-called Minkowski stress tensor that is usually written as:
The corresponding electromagnetic body force can be written as
which sometimes is referred to as the Korteweg-Helmholtz force. For homogeneous materials without deformation, one has ∇χ = 0. Hence, in the absence of free charges (ρe = 0), the body force becomes zero. Thus, the whole electromechanical load on the solid is due to the Maxwell stress jumps at the boundaries between domains with different material properties.
There are two most often used alternatives. The first one is called Einstein–Laub stress tensor:
This form is widely accepted in modern electroelasticity and material science, see Ref. 138. The corresponding body force can be written as:
which is also called Kelvin force. Note that it is nonzero as soon as there are electric field variation and polarization within the material:
The other alternative is Chu stress tensor:
(3-159)
and the corresponding electromagnetic body force is given by
Note that in contrast to the above equation, the expression for the stress tensor itself (Equation 3-159) seems to ignore the material polarization properties. However, if the frame difference is important because of the deformations, one has
(3-160)
The electric enthalpy can be written as
Then,
and the electromechanical second Piola–Kirchhoff stress tensor is given by
(3-161)
where σEM is given by Equation 3-159, which shows the consistency of the theory. The key assumption behind the derivation of Equation 3-161 is that the material components of the electric susceptibility χm are independent of deformations.
COMSOL Multiphysics provides a choice of the electromagnetic stress model, which is available in the Electromechanics coupling feature. Any of the above presented three options can be selected; the default choice is the Minkowski stress tensor.
References for the Electromechanics Interface
1. J.A. Stratton, Electromagnetic Theory, Cambridge, MA, 1941.
2. L.D. Landau and E.M. Lifshitz, Electrodynamics of Continuous Media, Pergamon Press, pp. 69–73, 1960.
3. D.J. Griffiths, “Resource Letter EM-1: Electromagnetic Momentum,” Am. J. Phys., vol. 80, pp. 7–18, 2012.
4. L. Dorfmann, R.W. Ogden, Mechanics and Electrodynamics of Electroelastic and Magnetoelastic Interactions, Springer, 2014.