The Rotating Frame feature exerts fictitious forces on particles that are moving in a rotating frame of reference. Optionally, it also applies an offset to the initial velocities of released particles, depending on whether their velocities are initialized with respect to the inertial (nonaccelerating) frame or the rotating (noninertial) frame. Additionally, when this feature is enabled, the particle trajectories are solved in the rotating frame of reference, and their corresponding positions and velocities in the inertial frame are also evaluated for use in other features such as the Magnetic Force.

Consider a particle of mass mp (SI unit: kg) moving in a noninertial frame of reference that is rotating at an angular velocity Ω (SI unit: rad/s) about a center of rotation with position rbp (SI unit: m). Note that Ω is a vector quantity that also indicates the orientation of the axis of rotation and the sense of rotation (clockwise or counterclockwise). A rotation matrix Rrot is introduced that maps the inertial (laboratory) and non-inertial (rotating) reference frames. Given the angle of rotation αfr, the rotation matrix Rrot is defined by the Rodrigues’ rotation formula,

Here, W denotes the antisymmetric matrix

where the axis of rotation is given by the unit vector [nx, ny, nz].

In 2D, Rrot simplifies to

The rotation angle αfr is governed by the ODE

The dependent variables q and v correspond to the noninertial reference frame. The displacement r (SI unit: m) of the particle is defined with respect to the center of rotation ,

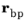
where q (SI unit: m) is the particle position. The equivalent dependent variables in the inertial reference frame qin and vin are evaluated as

where vf = Ω × r denotes the frame velocity at the particle position. When the Rotating Frame feature is active, it is possible to subtract the frame velocity from the initial particle velocity when releasing particles. This is equivalent to specifying the initial particle velocity with respect to the inertial frame. The relationship between the initial velocity in the inertial frame vi,in and in the rotating frame vi,rot is

The total fictitious force Ffr (SI unit: N) exerted on a particle in this noninertial frame of reference is (Ref. 1)

Additionally, the particles may be subject to additional external forces which are collectively represented as Fext (SI unit: N). The motion of a particle moving under the effect of these external and fictitious forces is governed by the Newton’s equations of motion

when the Newtonian formulation is used. Similarly, when the Newtonian, first order formulation is used, the equations of motion are

The rotation matrix in the above equations transform the external forces (applied in the inertial frame) onto the noninertial frame. The external forces are therefore computed in the inertial reference frame. Note that this means that the external forces that depend on particle velocities such as the Magnetic Force will use the variable vin instead of v. Similarly, forces that depend on field variables (and their derivatives) such as the velocity field in the Drag Force will evaluate the field variables (and their derivatives) at qin instead of q.