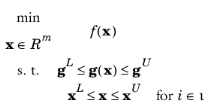The IPOPT Solver
The IPOPT solver uses a gradient-based optimization technique to find optimal solutions to a very general class of optimization problems. It requires external computation (analytically or seminumerically) for the gradients of both the objective function and all constraints.
The underlying algorithm is an implementation of an interior point line search filter for general nonlinear programming problems:
(5-6)
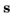
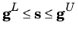
where f is the objective, x are the controls, g is the constraint function. IPOPT reformulates the problem to eliminate inequality constraints by introducing the slack variables, , with bounds, , and the auxiliary equation, g(x)=s. The equivalent reformulation is
which in terms of the augmented design variable, , and the equality constraints, , can be written as
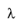
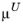
where and . The first-order optimality conditions for the problem (Karush–Kuhn–Tucker, KKT) become
(5-7)
(5-8)
(5-9)
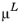
where , and are Lagrange variables associated with the equality and inequality constraints, respectively.
Termination
The error used for convergence depends on Equation 5-7, Equation 5-8 and Equation 5-9.
(5-10)
where sd and sc are internal scales that serve to avoid numerical problems
where . The convergence checks required for termination are
•
E≤tol
•
 ≤dual_inf_tol
•
≤constr_viol_tol
•
≤compl_inf_tol
The IPOPT log contains the error, , and the maximum infeasibility (MaxInfeas), .