
|
|
•
|
|
•
|
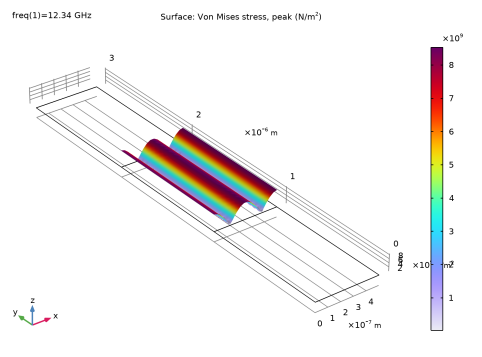
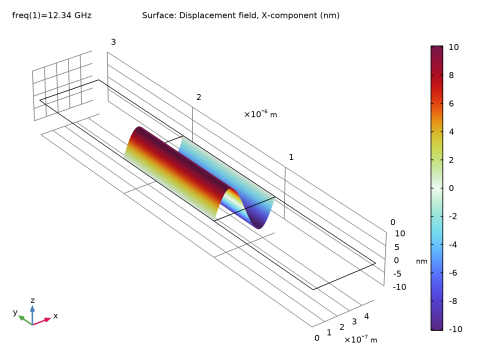
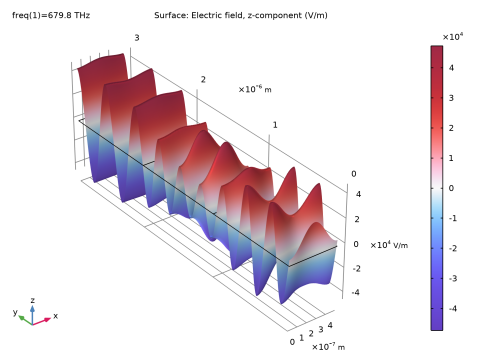
|
1
|
|
2
|
|
3
|
Click Add.
|
|
4
|
In the Select Physics tree, select Optics > Wave Optics > Electromagnetic Waves, Frequency Domain (ewfd).
|
|
5
|
Click Add.
|
|
6
|
Click
|
|
7
|
|
8
|
Click
|
|
1
|
|
2
|
|
3
|
Click
|
|
4
|
Browse to the model’s Application Libraries folder and double-click the file acousto_optic_modulator_parameters.txt.
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
Click to expand the Layers section. In the table, enter the following settings:
|
|
6
|
Select the Layers on top checkbox.
|
|
7
|
|
1
|
In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material.
|
|
2
|
|
3
|
Locate the Material Contents section. In the table, enter the following settings:
|
|
1
|
|
2
|
|
4
|
Locate the Material Contents section. In the table, enter the following settings:
|
|
6
|
|
7
|
|
9
|
Click OK.
|
|
1
|
|
2
|
|
4
|
Locate the Material Contents section. Click to select row number 4 in the table.
|
|
5
|
|
6
|
|
8
|
Click OK.
|
|
1
|
|
1
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
1
|
|
1
|
In the Model Builder window, under Component 1 (comp1) click Electromagnetic Waves, Frequency Domain (ewfd).
|
|
2
|
|
3
|
From the Electric field components solved for list, choose Out-of-plane vector, as the optical wave will be polarized in the z-direction.
|
|
1
|
|
2
|
|
3
|
|
4
|
Locate the Port Handling section. Click Add Diffraction Orders, to generate all the necessary diffraction orders to absorb all radiation that reaches the port boundaries.
|
|
1
|
|
3
|
|
4
|
Click to select the
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
In the Solve for column of the table, under Component 1 (comp1), clear the checkbox for Electromagnetic Waves, Frequency Domain (ewfd), to only solve for the Solid Mechanics interface in this study step.
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
Go to the Add Study window.
|
|
3
|
|
4
|
Find the Physics interfaces in study subsection. In the table, clear the Solve checkbox for Solid Mechanics (solid).
|
|
5
|
Click the Add Study button in the window toolbar.
|
|
6
|
|
1
|
|
2
|
|
3
|
|
4
|
Click to expand the Values of Dependent Variables section. Find the Values of variables not solved for subsection. From the Settings list, choose User controlled.
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
|
4
|
|
1
|
|
2
|
|
3
|
|
4
|
|
6
|
Select the Apply to dataset edges checkbox.
|
|
7
|
|
1
|
|
2
|
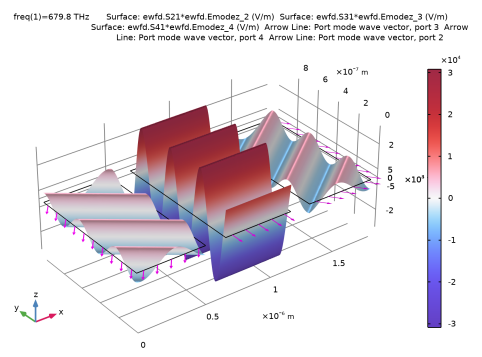
In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1) > Electromagnetic Waves, Frequency Domain > Ports > Electric mode fields > Electric mode field, port 2 - V/m > ewfd.Emodez_2 - Electric mode field, port 2, z-component. This represents the mode field of the zero-order port on the transmission side.
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
In the Model Builder window, under Results > Diffraction Orders right-click Surface 1 and choose Duplicate.
|
|
2
|
|
3
|
In the Expression text field, type ewfd.Emodez_3. This is the mode field of diffraction order m = -1 on the transmission side.
|
|
4
|
|
5
|
|
1
|
|
2
|
|
3
|
In the Expression text field, type ewfd.Emodez_4. This is the mode field of diffraction order m = 1 on the transmission side.
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
1
|
|
2
|
In the Settings window for Arrow Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1 (comp1) > Electromagnetic Waves, Frequency Domain > Ports > Wave vectors > ewfd.kModex_3,ewfd.kModey_3 - Port mode wave vector, port 3.
|
|
3
|
|
4
|
|
5
|
|
1
|
|
1
|
In the Model Builder window, under Results > Diffraction Orders right-click Arrow Line 1 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
1
|
|
2
|
|
3
|
Click to select the
|
|
1
|
In the Model Builder window, under Results > Diffraction Orders right-click Arrow Line 1 and choose Duplicate.
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|
|
7
|
|
1
|
|
2
|
|
3
|
Click to select the
|
|
1
|
|
2
|
|
3
|
Set the slider value to 5E-15.
|
|
1
|
|
2
|
|
1
|
|
2
|
|
3
|
|
4
|
|
5
|
|
6
|