At a three-phase boundary, it is necessary to add force terms to ensure that the fluid maintains a consistent contact angle. The forces acting at the contact point are applied to the fluid by the Contact Angle node (added per default under a Free Surface node). In equilibrium, the surface tension forces and the normal restoring force from the surface are in balance at a contact angle (θc), as shown in Figure 3-1. This equilibrium is expressed by Young’s equation, which considers the components of the forces in the plane of the surface:

where σ is the surface tension between the two fluids, γs1 is the surface energy density on the wetted side, and γs2 the surface energy density on the other side of the two-phase interface.

There is still debate in the literature as to precisely what occurs in nonequilibrium situations (for example, drop impact) when the physical contact angle deviates from the contact angle specified by Young’s equation. A simple approach, is to assume that the unbalanced part of the in-plane Young force acts on the fluid to move the contact angle toward its equilibrium value (Ref. 1). COMSOL Multiphysics employs this approach as it is physically motivated and is consistent with the thermodynamics allowed form of the boundary condition (Ref. 2, Ref. 3).

The normal force balance at the solid surface is handled by the wall boundary condition, which automatically prevents fluid flow across the solid boundary through a no-penetration condition. The wall fluid interface feature applies a force, fwf, on the fluid at the interface:

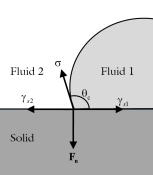
where θ is the actual contact angle and ms is the binormal to the solid surface.