Assuming that a model is invariant in the z direction, and symmetric with respect to the
xy–plane, then

. The radiative transfer equation can thus be solved for only half of the 3D directions for the discrete ordinates methods (DOM). For the
Si+ directions, the equation reads:
Note that the sum in the scattering term still contains all directions Sj, not only the ones with a positive
z component. Using
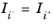
and since quadrature sets are built symmetric (
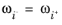
), the scattering term is then recast
The equation is now written only as a function of the radiative intensities associated to a positive z component direction, and only in the phase function do the negative
z component directions appear. The weights in 2D are redefined as the double of the 3D weights
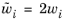
, such that, in the end, the 2D formulation of the DOM is:
In COMSOL Multiphysics, all phase functions ϕ(Sj, Si) can be rewritten as functions of
Sj ⋅ Si. For relatively simple phase functions, this allows for further simplification of the average between phase functions with positive and negative
z component, which can lead to the equation being written without any negative
z component directions. However, since more complex phase functions are also supported, this general form is preferred.
Using results from Equation 4-129 and
Equation 4-130 the DOM is formulated in 2D using only radiative intensities,
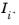
, on half of the 3D DOM directions,

, except for the scattering term.