Theory for Cell Periodicity
This section presents the underlying theory of the Cell Periodicity feature, and the resulting heat transfer equations that hold.
The heterogeneous properties of a material at the microscopic scale are often impractical for direct application at the macroscopic scale. In such cases, it becomes necessary to employ a homogeneous material model that incorporates appropriately equivalent properties.
The Cell Periodicity feature facilitates the evaluation of such average properties for heat transfer. It is based on the idea of a repeating unit cell (RUC) or a representative volume element (RVE). The cell is a microscopic domain that is representative for the material on a macroscopic length scale.
The terms RVE (Representative Volume Element) and RUC (Repeating Unit Cell) are frequently used interchangeably in the academic literature. Generally, an RVE describes a subvolume that characterizes heterogeneous materials with a statistically homogeneous microstructure. Conversely, the RUC is employed to represent subvolumes characterized by periodic patterns.
When dealing with materials characterized by a random distribution of particles, fibers, or pores, the appropriate subvolume to consider would be an RVE. To be numerically efficient, this RVE should be as small as possible, but sufficiently large to provide a representative sample for the determination of average material properties at a macroscopic scale.
If the material or lattice exhibits true periodicity, the suitable choice for representing a material subvolume would be an RUC, which repeats itself to uniformly fill the space with a repetitive pattern.
The distinction between RVEs and RUCs necessitates the application of different sets of boundary conditions. The Cell Periodicity node offers two distinct sets of boundary conditions, namely Uniform temperature gradient and Periodic temperature, designed to suit these subvolumes respectively.
Homogenization method
The homogenization method introduces two scales: a macroscale and a microscale. The macroscale usually refers to the homogenized continuous medium, and the microscale to the heterogeneous cell. The macroscopic conductive heat flux qavg and the macroscopic temperature gradient ∇Tavg are derived by averaging the conductive heat flux and temperature gradient in the cell:
(4-93) and
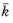
where V is the volume of the cell. The macroscopic thermal conductivity tensor of the homogenized continuum is then defined by
(4-94)
Uniform temperature gradient boundary condition
Let’s consider the temperature field on the outer boundaries of a RVE written as:
where ∇T0 is a uniform temperature gradient, and X is the position. By applying the divergence theorem, it can be demonstrated that:
The volume-averaged temperature gradient in the RVE is then equal to the uniform temperature gradient applied on its outer boundaries, irrespective of the constitution of the material subvolume.
Periodic temperature boundary conditions
For a periodic structure that consists of an array of RUC, the temperature field over cell outer boundaries is written as:
where ∇T0 is a uniform average temperature gradient, X is the position, and T* is a function that is periodic from one cell to another. Given that the array of cells forms a continuous structure, it is essential to ensure continuity of temperature across the boundaries between these cells. The boundaries in a Boundary Pair subnode must therefore always appear in parallel pairs. One of them is labeled as source and the other as destination. The temperature on a pair of parallel (and opposite) boundaries can be written as:
and
where Xdst and Tdst are the position and temperature on the destination side, and Xsrc and Tsrc are the position and temperature on the source side.
Hence, the temperature boundary condition is established by:
As for the uniform temperature gradient boundary condition, applying the divergence theorem leads to:
The volume-averaged temperature gradient in the RUC is also equal to the uniform temperature gradient applied on its outer boundaries, irrespective of the constitution of the material subvolume. In that case, it is required to constrain the temperature at one point of the RUC to ensure uniqueness of the solution.
Prescribed average temperature gradient
In order to determine the homogeneous thermal conductivity tensor of a heterogeneous material, the material is subjected on its outer boundaries to a non-zero uniform temperature gradient ∇T0 in each direction, one-by-one, while keeping the other components equal to zero. With both uniform temperature gradient and periodic temperature boundary conditions, the global average temperature gradient ∇Tavg is equal to this uniform temperature gradient ∇T0 and is then a user input. 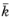The average conductive heat flux qavg is computed from Equation 4-93, and the thermal conductivity tensor is obtained from Equation 4-94.