The electrochemical potential μi (J/mol) of the individual species are defined as

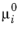
where R is the molar gas constant (8.31 J/mol/K), is the electrochemical potential with respect to some reference state, T is the temperature (K), xi is the molar fraction, the λi the species activity coefficient (dimensionless) and Φ (V) is the solution potential.

For ideal conditions, the species activity coefficients equal unity. For nonideal solutions, two issues experimental arise in relation to the definition of individual species activity coefficients. The first is that, since charge separation is virtually impossible to achieve in a solution, it is hard to assess the chemical activity of individual ions experimentally. The second is that, since all major species in the solution are accounted for, one cannot alter the concentration of a single species (or electrolyte salt) with out changing the concentration of at least one other compound. To circumvent these issues, activity coefficients are defined in the form of (n − 1)(n − 2)/2 electroneutral component Darken factors (dimensionless) in an electrolyte component basis as

where the derivative should be made keeping the temperature, pressure and all electrolyte components but the ones with index j and k constant. In the Concentrated Electrolyte Transport interface, the index k equals the index of the electrolyte component taken from the molar fraction constraint.

where Dij (m2/s) are the binary Maxwell–Stefan diffusivity coefficients. The above equation system is transformed and inverted in order express the electrolyte component fluxes in terms of the gradients of the electrolyte component chemical potentials.