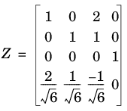The Concentrated Electrolyte Transport interface defines the transport of a total number of n either positively (cations), negatively (anions), or neutrally charged species in an electrolyte phase. At least one cation and one anion must be defined.

The mathematical framework makes use of a number of electrolyte components that are constructed by forming a set of n − 1 neutral salts based on the n electrolyte species. It should be noted that the purpose of the neutral electrolyte components is to form a basis for the mathematical framework only; they do not necessarily have any physical correspondence as a real salt in nature. As an example, for an electrolyte composed of the four species Mg2+, H+, OH-, and H2O, the set Mg-(OH)2, H-OH, and H2O form the corresponding electrolyte component basis.

The mathematical framework expresses variables either in using the individual electrolyte species as a basis or the electrolyte components. The index i, j, or k is used generally to define the index of either a species or an electrolyte component. Symbols referring to an electrolyte component are denoted by a tilde (~) on top of the greek or roman character, whereas indexed symbols without the tilde refer to a species.

Transformations between the species and electrolyte component basis are made by the use of a (n × n) transformation matrix Z, which consists n − 1 rows that define the stoichiometric coefficients of the species for each electroneutral salt, and with an nth row defining the individual species charges, divided by the norm of the charge vector.

For the Mg2+, OH-, H+, and H2O example, the Z matrix would look like

For instance, the molar weights (kg/mol) of the electrolyte component salts can be computed from the first n − 1 rows of the column resulting from the matrix multiplication

where M = [M1 M2 … Mn]T is a column vector of the defined by the individual species molar masses Mi (kg/mol).

Also the inverse transpose matrix Z−T is used for various variable basis transformations.

where zi (dimensionless) are the individual species charges, and ci the molar concentrations (mol/m3).

Electroneutrality in combination with a volumetric equation of state (see next section), assuming all major constituents of the electrolyte to be included in the electrolyte model, allows for reducing the number of dependent variables by 2, resulting in an equation system consisting of n − 1 electrolyte component fraction (dimensionless) and one electrolyte potential ϕl (V) dependent variables.